
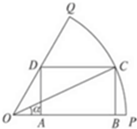
 如圖,已知OPQ是半徑為1,圓心角為$\frac{π}{3}$的扇形,C是扇形弧上的動點,四邊形ABCD是扇形的內接矩形,記∠COP=α,矩形的面積為S;
如圖,已知OPQ是半徑為1,圓心角為$\frac{π}{3}$的扇形,C是扇形弧上的動點,四邊形ABCD是扇形的內接矩形,記∠COP=α,矩形的面積為S;分析 (1)先把矩形的各個邊長用角α表示出來,進而表示出矩形的面積,即可得解;
(2)利用三角函數恒等變換的應用化簡后,再利用角α的范圍,結合正弦函數的性質可求矩形面積的最大值即可.
解答 (本小題滿分12分)
解:(1)在直角△OBC中,BC=sinα,OB=cosα,…(1分)
在直角△OAD中,$\frac{DA}{OA}=tan\frac{π}{3}=\sqrt{3}$,…(2分)
所以$OA=\frac{{\sqrt{3}}}{3}DA=\frac{{\sqrt{3}}}{3}BC=\frac{{\sqrt{3}}}{3}sinα$,…(3分)
所以$AB=OB-OA=cosα-\frac{{\sqrt{3}}}{3}sinα$,…(4分)
所以矩形ABCD的面積$S=AB×BC=(cosα-\frac{{\sqrt{3}}}{3}sinα)•sinα$,$(0<α<\frac{π}{3})$…(6分)
(2)由$S=AB×BC=(cosα-\frac{{\sqrt{3}}}{3}sinα)•sinα=sinαcosα-\frac{{\sqrt{3}}}{3}{sin^2}α$=$\frac{1}{2}sin2α-\frac{{\sqrt{3}}}{3}×\frac{1-cos2α}{2}=\frac{1}{2}sin2α+\frac{{\sqrt{3}}}{6}cos2α-\frac{{\sqrt{3}}}{6}$…(8分)
=$\frac{{\sqrt{3}}}{3}(\frac{{\sqrt{3}}}{2}sin2α+\frac{1}{2}cos2α)-\frac{{\sqrt{3}}}{6}=\frac{{\sqrt{3}}}{3}sin(2α+\frac{π}{6})-\frac{{\sqrt{3}}}{6}$,…(10分)
∵$0<α<\frac{π}{3}$,
∴$當2α+\frac{π}{6}=\frac{π}{2}時$,即$α=\frac{π}{6}時$,矩形ABCD的面積S取得最大值為$\frac{{\sqrt{3}}}{3}-\frac{{\sqrt{3}}}{6}=\frac{{\sqrt{3}}}{6}$.…(12分)
點評 本題考查在實際問題中建立三角函數模型,求解問題的關鍵是根據圖形建立起三角模型,將三角模型用所學的恒等式變換公式進行化簡,考查了轉化思想和數形結合思想,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
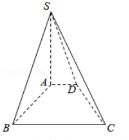 已知四棱錐S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.
已知四棱錐S-ABCD中,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,SA=AB=BC=2,AD=1,SA⊥底面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
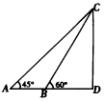 如圖所示,A,B,D在地平面同一直線上,AB=20,從A,B兩地測得C點的仰角分別為45°和60°,則C點離地面的高CD等于( )
如圖所示,A,B,D在地平面同一直線上,AB=20,從A,B兩地測得C點的仰角分別為45°和60°,則C點離地面的高CD等于( )| A. | $10(\sqrt{3}-1)$ | B. | $10(\sqrt{3}+1)$ | C. | $10(3-\sqrt{3})$ | D. | $10(3+\sqrt{3})$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com