
分析 由題意軸截面為正方形 EFGH 的圓柱的體積為2π,正方形的邊長為1.可以從E點沿圓柱的側面到相對頂點G的最短距離為圓柱側面展開圖一個頂點到對邊中點的距離,利用勾股定理就可以求出其值.
解答 解:軸截面為正方形 EFGH 的圓柱的體積為2π,正方形的邊長為1
從E點沿圓柱的側面到相對頂點G的最短距離即為圓柱側面展開圖一個頂點到對邊中點的距離,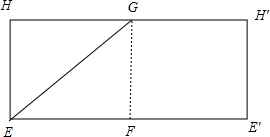
∵圓柱的軸截面的邊長為1,
故GF=2,EF=π,
∴EG=$\sqrt{{π}^{2}+4}$,
故答案為:$\sqrt{{π}^{2}+4}$.
點評 本題考查的知識點是旋轉體的展開圖,其中將問題轉化為平面上兩點之間的距離線段最短是解答的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
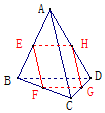 已知E,F,G,H分別是空間四邊形四條邊AB,BC,CD,DA的中點,
已知E,F,G,H分別是空間四邊形四條邊AB,BC,CD,DA的中點,查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1,2,3,4,5 | B. | 4,14,24,34,44 | C. | 2,4,6,8,10 | D. | 4,13,22,31,40 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 2,3 | C. | 1,4 | D. | 1,2,3,4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
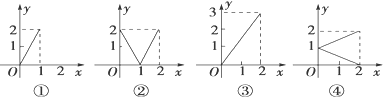
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com