Question

6．（1）已知向量$\overrightarrow{a}$=（2，-3），$\overrightarrow{MN}$與$\overrightarrow a$垂直，且|${\overrightarrow{MN}}$|=3$\sqrt{13}$，若點M的坐標為（-3，2），求$\overrightarrow{ON}$（其中O為坐標原點）；
（2）設O為△ABC的外心（三角形外接圓的圓心），若$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|${\overrightarrow{AB}}$|²，求$\frac{{\left|{\overrightarrow{AC}}\right|}}{{\left|{\overrightarrow{AB}}\right|}}$的值．

Answer 1

分析 （1）設$\overrightarrow{ON}$=（a，b），依題意，可得2（a+3）-3（b-2）=0，且（a+3）²+（b-2）²=117，解之即可求得$\overrightarrow{ON}$；
（2）$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|${\overrightarrow{AB}}$|²⇒設2$\overrightarrow{AO}$•$\overrightarrow{BC}$=|${\overrightarrow{AB}}$|²，延長AO與圓O交于點D，利用向量的數量積的幾何意義可求得b²=2c²，從而可得$\frac{{\left|{\overrightarrow{AC}}\right|}}{{\left|{\overrightarrow{AB}}\right|}}$的值．

解答 解：（1）設$\overrightarrow{ON}$=（a，b），∵M的坐標為（-3，2），
∴$\overrightarrow{MN}$=（a+3，b-2），
∵$\overrightarrow{MN}$與$\overrightarrow a$垂直，且|${\overrightarrow{MN}}$|=3$\sqrt{13}$，
∴2（a+3）-3（b-2）=0，且（a+3）²+（b-2）²=117，
解得：a=6，b=8或a=-12，b=-4．
∴$\overrightarrow{ON}=（6，8），\overrightarrow{ON}=（-12，-4）$．
（2）∵O為△ABC的外心（三角形外接圓的圓心），
$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|${\overrightarrow{AB}}$|²，即2$\overrightarrow{AO}$•$\overrightarrow{BC}$=|${\overrightarrow{AB}}$|²，延長AO與圓O交于點D，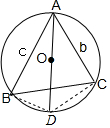

則2$\overrightarrow{AO}$•$\overrightarrow{BC}$=|${\overrightarrow{AB}}$|²?$\overrightarrow{AD}$•（$\overrightarrow{AC}$-$\overrightarrow{AB}$）=|$\overrightarrow{AB}$|²，
即b•（|AD|cos∠CAD）-c•（|AD|cos∠BAD）=b²-c²=c²，
∴b²=2c²，
∴$\frac{{\left|{\overrightarrow{AC}}\right|}}{{\left|{\overrightarrow{AB}}\right|}}$=$\frac{b}{c}$=$\sqrt{2}$．

點評 本題考查平面向量數量積的坐標運算，突出考查向量共線與垂直的坐標運算，由$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\frac{1}{2}$|${\overrightarrow{AB}}$|²⇒b²=2c²是關鍵，也是難點，考查數形結合思想與等價轉化思想的綜合運用，屬于難題．