
(本小題滿分14分)設a為常數,且 .
.
(1)解關于x的不等式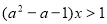 ;
;
(2)解關于x的不等式組 .
.
(1)①當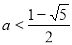 時,解原不等式,得
時,解原不等式,得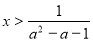 ,即其解集為
,即其解集為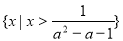 ;
;
②當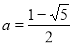 時,解原不等式,得無解,即其解集為
時,解原不等式,得無解,即其解集為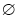 ;
;
③當 時,解原不等式,得
時,解原不等式,得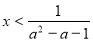 ,即其解集為
,即其解集為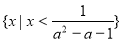
(2)當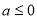 時,原不等式組的解集為
時,原不等式組的解集為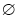 ;當
;當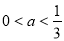 時,原不等式組的解集為
時,原不等式組的解集為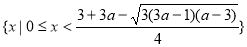 ;當
;當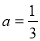 時,原不等式組的解集為
時,原不等式組的解集為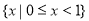 ;當
;當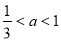 時,原不等式組的解集為
時,原不等式組的解集為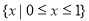 .
.
【解析】
試題分析:(1)解決與之相關的問題時,可利用函數與方程的思想、化歸的思想將問題轉化,結合二次函數的圖象來解決;(2)解含參數的一元二次不等式分類討論的依據:一是二次項中若含有參數應討論是小于0,等于0,還是大于0,然后將不等式轉化為二次項系數為正的形式,二是當不等式對應的方程的根個數不確定時,討論判別式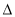 與0的關系,三是確定無根時可直接寫出解集,確定方程有兩個根時,要討論兩根的大小關系,從而確定解集;(3)討論時注意找臨界條件討論.
與0的關系,三是確定無根時可直接寫出解集,確定方程有兩個根時,要討論兩根的大小關系,從而確定解集;(3)討論時注意找臨界條件討論.
試題解析:【解析】
(1)令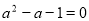 ,解得
,解得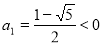 ,
,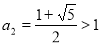 . (1分)
. (1分)
①當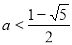 時,解原不等式,得
時,解原不等式,得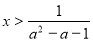 ,即其解集為
,即其解集為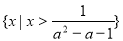 ;
;
(2分)
②當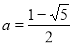 時,解原不等式,得無解,即其解集為
時,解原不等式,得無解,即其解集為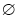 ; (3分)
; (3分)
③當 時,解原不等式,得
時,解原不等式,得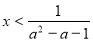 ,即其解集為
,即其解集為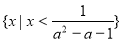 .
.
(4分)
(2)依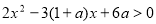 (*),令
(*),令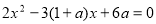 (**),
(**),
可得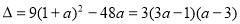 . (5分)
. (5分)
①當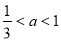 時,
時,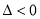 ,此時方程(**)無解,解不等式(*),得
,此時方程(**)無解,解不等式(*),得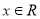 ,故原不等式組的解集為
,故原不等式組的解集為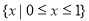 ; (6分)
; (6分)
②當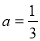 時,
時,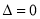 , 此時方程(**)有兩個相等的實根
, 此時方程(**)有兩個相等的實根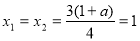 ,解不等式(*),得
,解不等式(*),得 ,故原不等式組的解集為
,故原不等式組的解集為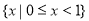 ; (7分)
; (7分)
③當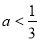 時,
時,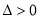 ,此時方程(**)有兩個不等的實根
,此時方程(**)有兩個不等的實根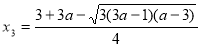 ,
,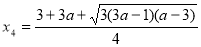 ,且
,且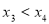 ,解不等式(*),得
,解不等式(*),得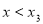 或
或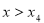 .
.
(8分)
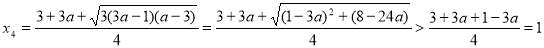 ,
,
(9分)
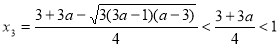 , (10分)
, (10分)
且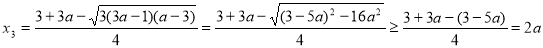 ,
,
(11分)
所以當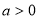 ,可得
,可得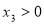 ;又當
;又當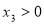 ,可得
,可得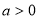 ,故
,故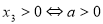 ,(12分)
,(12分)
所以(ⅰ)當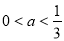 時,原不等式組的解集為
時,原不等式組的解集為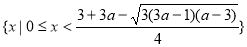 ;
;
(13分)
(ⅱ)當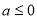 時,原不等式組的解集為
時,原不等式組的解集為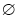 . (14分)
. (14分)
綜上,當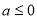 時,原不等式組的解集為
時,原不等式組的解集為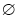 ;當
;當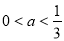 時,原不等式組的解集為
時,原不等式組的解集為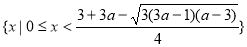 ;當
;當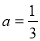 時,原不等式組的解集為
時,原不等式組的解集為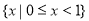 ;當
;當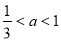 時,原不等式組的解集為
時,原不等式組的解集為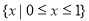 .
.
考點:1、含參數的一元二次不等式的解法;2、分類討論的思想.


 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:高中數學 來源:2014-2015學年河南省高二上學期第一次月考試理科數學卷(解析版) 題型:選擇題
《萊因德紙草書》是世界上最古老的數學著作之一,書中有這樣的一道題目:把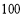 個面包分給
個面包分給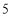 個人,使每人所得成等差數列,且使較大的三份之和的
個人,使每人所得成等差數列,且使較大的三份之和的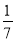 是較小的兩份之和,則最小的
是較小的兩份之和,則最小的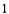 份為( )
份為( )
A.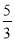 B.
B.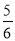 C.
C.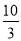 D.
D.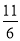
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省山一等七校高三12月聯考理科數學試卷(解析版) 題型:選擇題
已知三個正態分布密度函數 (
(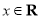 ,
,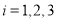 )的圖象如圖
)的圖象如圖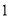 所示,則( )
所示,則( )

A. ,
,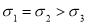
B.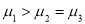 ,
,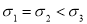
C. ,
,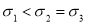
D.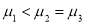 ,
,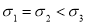
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省肇慶市畢業班第一次統一檢測文科數學試卷(解析版) 題型:解答題
(本小題滿分12分)某工廠的A、B、C三個不同車間生產同一產品的數量(單位:件)如下表所示. 質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測.
車間 | A | B | C |
數量 | 50 | 150 | 100 |
(1)求這6件樣品中來自A、B、C各車間產品的數量;
(2)若在這6件樣品中隨機抽取2件進行進一步檢測,求這2件商品來自相同車間的概率.
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省肇慶市畢業班第一次統一檢測文科數學試卷(解析版) 題型:選擇題
執行如圖所示的程序框圖輸出的結果是
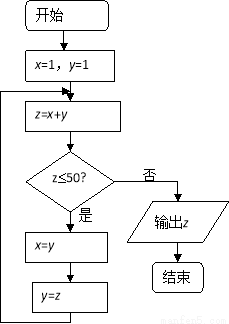
A.55 B.65
C.78 D.89
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com