
(本小題滿分12分)某工廠的A、B、C三個不同車間生產同一產品的數(shù)量(單位:件)如下表所示. 質檢人員用分層抽樣的方法從這些產品中共抽取6件樣品進行檢測.
車間 | A | B | C |
數(shù)量 | 50 | 150 | 100 |
(1)求這6件樣品中來自A、B、C各車間產品的數(shù)量;
(2)若在這6件樣品中隨機抽取2件進行進一步檢測,求這2件商品來自相同車間的概率.
(1)這6件樣品中來自A、B、C各車間產品的數(shù)量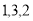 ;(2)
;(2)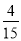
【解析】
試題分析:(1)古典概型的概率問題,關鍵是正確找出基本事件總數(shù)和所求事件包含的基本事件數(shù),然后利用古典概型的概率計算公式計算;(2)當基本事件總數(shù)較少時,用列舉法把所有的基本事件一一列舉出來,要做到不重不漏,有時可借助列表,樹狀圖列舉,當基本事件總數(shù)較多時,注意去分排列與組合;(3)注意判斷是古典概型還是幾何概型,基本事件前者是有限的,后者是無限的,兩者都是等可能性.(4)在幾何概型中注意區(qū)域是線段,平面圖形,立體圖形.
試題解析:(1)因為樣本容量與總體中的個體數(shù)的比是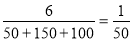 ,(2分)
,(2分)
所以A車間產品被選取的件數(shù)為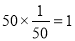 , (3分)
, (3分)
B車間產品被選取的件數(shù)為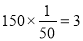 , (4分)
, (4分)
C車間產品被選取的件數(shù)為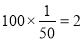 . (5分)
. (5分)
(2)設6件來自A、B、C三個車間的樣品分別為:A;B1,B2,B3;C1,C2.
則從6件樣品中抽取的這2件產品構成的所有基本事件為:(A,B1),(A,B2),(A,B3),(A,C1),(A,C2),(B1,B2),(B1,B3),(B1,C1),(B1,C2),(B2,B3),(B2,C1),(B2,C2),(B3,C1),(B3,C2),(C1,C2),共15個. (8分)
每個樣品被抽到的機會均等,因此這些基本事件的出現(xiàn)是等可能的. 記事件D:“抽取的這2件產品來自相同車間”,則事件D包含的基本事件有:(B1,B2),(B1,B3),(B2,B3),(C1,C2),共4個.
所以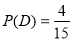 ,即這2件產品來自相同車間的概率為
,即這2件產品來自相同車間的概率為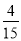 . (12分)
. (12分)
考點:1、分層抽樣的應用;2、利用古典概型求隨機事件的概率.


科目:高中數(shù)學 來源:2014-2015學年河南省高二上學期第一次月考試理科數(shù)學卷(解析版) 題型:選擇題
在等差數(shù)列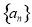 中,
中,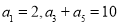 ,則
,則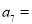 ( )
( )
A.5 B.8 C.10 D.14
查看答案和解析>>
科目:高中數(shù)學 來源:2014-2015學年廣東省山一等七校高三12月聯(lián)考文科數(shù)學試卷(解析版) 題型:選擇題
一枚硬幣連擲2次,只有一次出現(xiàn)正面的概率為( )
A.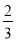 B.
B.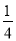 C.
C.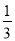 D.
D.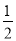
查看答案和解析>>
科目:高中數(shù)學 來源:2014-2015學年廣東省山一等七校高三12月聯(lián)考理科數(shù)學試卷(解析版) 題型:選擇題
已知雙曲線的中心在原點,一個焦點為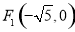 ,點
,點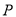 在雙曲線上,且線段
在雙曲線上,且線段 的中點坐標為
的中點坐標為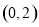 ,則此雙曲線的方程是( )
,則此雙曲線的方程是( )
A.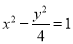 B.
B.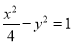 C.
C.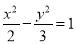 D.
D.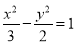
查看答案和解析>>
科目:高中數(shù)學 來源:2014-2015學年廣東省肇慶市畢業(yè)班第一次統(tǒng)一檢測文科數(shù)學試卷(解析版) 題型:解答題
(本小題滿分14分)設a為常數(shù),且 .
.
(1)解關于x的不等式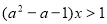 ;
;
(2)解關于x的不等式組 .
.
查看答案和解析>>
科目:高中數(shù)學 來源:2014-2015學年廣東省肇慶市畢業(yè)班第一次統(tǒng)一檢測文科數(shù)學試卷(解析版) 題型:選擇題
設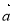 ,
,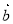 為非零向量,
為非零向量,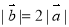 ,兩組向量
,兩組向量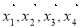 和
和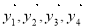 均由2個
均由2個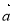 和2個
和2個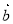 排列而成. 若
排列而成. 若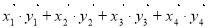 所有可能取值中的最小值為
所有可能取值中的最小值為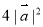 ,則
,則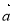 與
與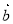 的夾角為
的夾角為
A.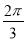 B.
B.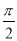 C.
C.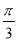 D.
D.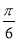
查看答案和解析>>
科目:高中數(shù)學 來源:2014-2015學年廣東省肇慶市畢業(yè)班第一次統(tǒng)一檢測理科數(shù)學試卷(解析版) 題型:選擇題
一個幾何體的三視圖如圖所示,其中正視圖和側視圖是腰長為1的兩個全等的等腰直角三角形,則該幾何體的外接球的表面積為

A.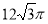 B.
B.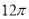 C.
C.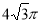 D.
D.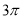
查看答案和解析>>
科目:高中數(shù)學 來源:2014-2015學年福建省四地六校高三上學期第三次月考理科數(shù)學試卷(解析版) 題型:選擇題
某同學在研究函數(shù)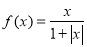 (
(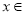 R)時,分別給出下面幾個結論:
R)時,分別給出下面幾個結論:
①等式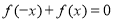 在
在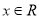 時恒成立;
時恒成立;
②函數(shù) f (x)的值域為 (-1,1);
③若x1≠x2,則一定有f (x1)≠f (x2);
④函數(shù)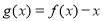 在
在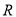 上有三個零點.
上有三個零點.
其中正確結論的序號是( )
A.①② B.①②③ C.①③④ D.①②③④
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com