Question

17．雙曲線C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦點和虛軸上的一個端點分別為F，A，點P為雙曲線C左支上一點，若△APF周長的最小值為6b，則雙曲線C的離心率為（　　）

• A． $\frac{\sqrt{56}}{8}$
• B． $\frac{\sqrt{85}}{7}$
• C． $\frac{\sqrt{85}}{6}$
• D． $\frac{\sqrt{13}}{3}$

Answer 1

分析 由題意求得A，F的坐標，設出F'，運用雙曲線的定義可得|PF|=|PF'|+2a，則△APF的周長為|PA|+|PF|+|AF|=|PA|+|PF'|+2a+$\sqrt{{b}^{2}+{c}^{2}}$，運用三點共線取得最小值，可得6a=7b，由a，b，c的關系，結合離心率公式，計算即可得到所求值．

解答 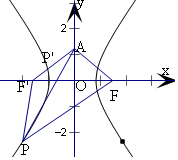解：由題意可得A（0，b），F（c，0），設F'（-c，0），
由雙曲線的定義可得|PF|-|PF'|=2a，
|PF|=|PF'|+2a，
|AF|=|AF'|=$\sqrt{{b}^{2}+{c}^{2}}$，
則△APF的周長為|PA|+|PF|+|AF||=|PA|+|PF'|+2a+|AF'|
≥2|AF'|+2a，
當且僅當A，P，F'共線，取得最小值，且為2a+2$\sqrt{{b}^{2}+{c}^{2}}$，
由題意可得6b=2a+2$\sqrt{{b}^{2}+{c}^{2}}$，
即b=$\frac{6}{7}$a，
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{\sqrt{85}}{7}$a，
則e=$\frac{c}{a}$=$\frac{\sqrt{85}}{7}$，
故選：B．

點評 本題考查雙曲線的離心率的求法，注意運用雙曲線的定義和轉化為三點共線取得最小值，考查運算能力，屬于中檔題．