
分析 由題意畫出圖形,可知要使四邊形PACB面積最小,則P為過圓心作直線3x+4y+8=0的垂線得垂足,由點到直線的距離公式求得PC,再由勾股定理得弦長,代入三角形面積公式得答案.
解答 解:如圖,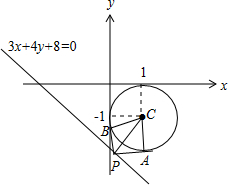
直線3x+4y+8=0與圓x2+y2-2x+2y+1=0相離,
化圓x2+y2-2x+2y+1=0為(x-1)2+(y+1)2=1,圓心坐標為C(1,-1),半徑為1.
連接CA,CB,則CA⊥PA,CB⊥PB,
則四邊形PACB的面積等于兩個全等直角三角形PAC與PBC的面積和.
∵AC是半徑,為定值1,要使三角形PAC的面積最小,則PC最小,
|PC|=$\frac{|3×1+4×(-1)+8|}{\sqrt{{3}^{2}+{4}^{2}}}=\frac{7}{5}$,
∴|PA|=$\sqrt{(\frac{7}{5})^{2}-{1}^{2}}=\frac{2\sqrt{6}}{5}$.
∴四邊形PACB面積的最小值為2×$\frac{1}{2}×1×\frac{2\sqrt{6}}{5}=\frac{2\sqrt{6}}{5}$.
故答案為:$\frac{2\sqrt{6}}{5}$.
點評 本題考查直線與圓位置關系的應用,考查數形結合的解題思想方法,屬于中檔題.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1或$\sqrt{3}$ | B. | 1或3 | C. | -2或6 | D. | 0或4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
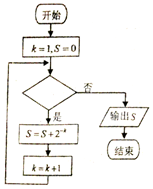
| A. | k≤8? | B. | k≤9? | C. | k≤10? | D. | k≤11? |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | n≤97 | B. | n≤98 | C. | n≤99 | D. | n≤100 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com