
甲、乙、丙三人參加某次招聘會,假設甲能被聘用的概率是 ,甲、丙兩人同時不能被聘用的概率是
,甲、丙兩人同時不能被聘用的概率是 ,乙、丙兩人同時能被聘用的概率為
,乙、丙兩人同時能被聘用的概率為 ,且三人各自能否被聘用相互獨立.
,且三人各自能否被聘用相互獨立.
(1)求乙、丙兩人各自被聘用的概率;
(2)設 為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求
為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求 的分布列與均值(數學期望).
的分布列與均值(數學期望).
(1)乙、丙兩人各自被聘用的概率分別為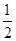 、
、 ;(2)詳見解析.
;(2)詳見解析.
解析試題分析:(1)分別設乙、丙兩人各自被聘用的概率為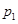 、
、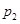 ,利用事件的獨立性列出相應的方程進行求解,從而得出乙、丙兩人各自被聘用的概率;(2)先列舉出隨機變量
,利用事件的獨立性列出相應的方程進行求解,從而得出乙、丙兩人各自被聘用的概率;(2)先列舉出隨機變量 的可能取值,并根據事件的獨立性求出
的可能取值,并根據事件的獨立性求出 在相應條件的概率,列出分布列并求出隨機變量
在相應條件的概率,列出分布列并求出隨機變量 的均值(即數學期望).
的均值(即數學期望).
試題解析:(1)設乙、丙兩人各自被聘用的概率分別為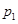 、
、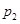 ,
,
則甲、丙兩人同時不能被聘用的概率是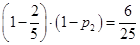 ,解得
,解得 ,
,
乙、丙兩人同時能被聘用的概率為 ,
,
因此乙、丙兩人各自被聘用的概率分別為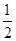 、
、 ;
;
(2) 的可能取值有
的可能取值有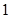 、
、 ,
,
則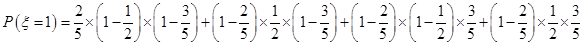
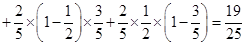 ,
,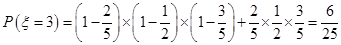 ,
,
因此隨機變量 的分布列如下表所示
的分布列如下表所示
所以隨機變量
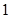


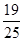

 的均值(即數學期望)
的均值(即數學期望)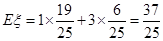 .
.
考點:1.獨立事件概率的計算;2.離散型隨機變量的概率分布列與數學期望


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案科目:高中數學 來源: 題型:解答題
某飲料公司對一名員工進行測試以便確定其考評級別.公司準備了兩種不同的飲料共5杯,其顏色完全相同,并且其中3杯為A飲料,另外2杯為B飲料,公司要求此員工一一品嘗后,從5杯飲料中選出3杯A飲料.若該員工3杯都選對,則評為優秀;若3杯選對2杯,則評為良好;否則評為合格.假設此人對A和B兩種飲料沒有鑒別能力.
(1)求此人被評為優秀的概率;
(2)求此人被評為良好及以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
中國男子籃球職業聯賽總決賽采用七場四勝制(即先勝四場者獲勝).進入總決賽的甲乙兩隊中,若每一場比賽甲隊獲勝的概率為 ,乙隊獲勝的概率為
,乙隊獲勝的概率為 ,假設每場比賽的結果互相獨立.現已賽完兩場,乙隊以
,假設每場比賽的結果互相獨立.現已賽完兩場,乙隊以 暫時領先.
暫時領先.
(1)求甲隊獲得這次比賽勝利的概率;
(2)設比賽結束時兩隊比賽的場數為隨機變量 ,求隨機變量
,求隨機變量 的分布列和數學期望
的分布列和數學期望 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在對某漁業產品的質量調研中,從甲、乙兩地出產的該產品中各隨機抽取10件,測量該產品中某種元素的含量(單位:毫克).下表是測量數據的莖葉圖: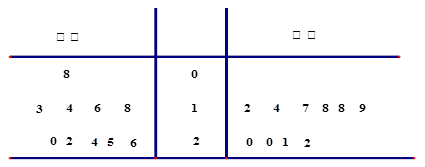
規定:當產品中的此種元素含量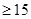 毫克時為優質品.
毫克時為優質品.
(1)試用上述樣本數據估計甲、乙兩地該產品的優質品率(優質品件數/總件數);
(2)從乙地抽出的上述10件產品中,隨機抽取3件,求抽到的3件產品中優質品數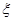 的分布列及數學期望
的分布列及數學期望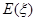 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某高校在202年自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組:第1組[75,80),第2組[80,85), 第3組[85,90),第4組[90,95),第5組[95,100]得到的頻率分布直方圖如圖所示.
(1)分別求第3,4,5組的頻率;
(2)若該校決定在筆試成績高的第3,4,5組中用分層抽樣抽取6名學生進入第二輪面試,
(ⅰ)已知學生甲和學生乙的成績均在第三組,求學生甲和學生乙同時進入第二輪面試的概率;
(ⅱ)學校決定在這6名學生中隨機抽取2名學生接受考官D的面試,設第4組中有 名學生被考官D面試,求
名學生被考官D面試,求 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一汽車廠生產A,B,C三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如表所示(單位:輛),若按A,B,C三類用分層抽樣的方法在這個月生產的轎車中抽取50輛,則A類轎車有10輛.
| | 轎車A | 轎車B | 轎車C |
| 舒適型 | 100 | 150 | z |
| 標準型 | 300 | 450 | 600 |
 .記這8輛轎車的得分的平均數為
.記這8輛轎車的得分的平均數為 ,定義事件
,定義事件 {
{ ,且函數
,且函數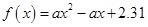 沒有零點},求事件
沒有零點},求事件 發生的概率.
發生的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工科院校對A,B兩個專業的男女生人數進行調查,得到如下的列聯表:
| | 專業A | 專業B | 總計 |
| 女生 | 12 | 4 | 16 |
| 男生 | 38 | 46 | 84 |
| 總計 | 50 | 50 | 100 |

| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一汽車廠生產A,B,C三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如表所示(單位輛),若按A,B,C三類用分層抽樣的方法在這個月生產的轎車中抽取50輛,則A類轎車有10輛
| | 轎車A | 轎車B | 轎車C |
| 舒適型 | 100 | 150 | z |
| 標準型 | 300 | 450 | 600 |
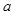 記這8輛轎車的得分的平均數為
記這8輛轎車的得分的平均數為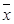 ,定義事件
,定義事件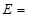 {
{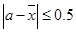 ,且函數
,且函數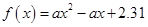 沒有零點},求事件
沒有零點},求事件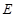 發生的概率
發生的概率 查看答案和解析>>
科目:高中數學 來源: 題型:解答題
“拋階磚”是國外游樂場的典型游戲之一.參與者只須將手上的“金幣”(設“金幣”的半徑為1)拋向離身邊若干距離的階磚平面上,拋出的“金幣”若恰好落在任何一個階磚(邊長為2.1的正方形)的范圍內(不與階磚相連的線重疊),便可獲大獎.不少人被高額獎金所吸引,紛紛參與此游戲但很少有人得到獎品,請用所學的概率知識解釋這是為什么.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com