
一汽車廠生產A,B,C三類轎車,每類轎車均有舒適型和標準型兩種型號,某月的產量如表所示(單位:輛),若按A,B,C三類用分層抽樣的方法在這個月生產的轎車中抽取50輛,則A類轎車有10輛.
| | 轎車A | 轎車B | 轎車C |
| 舒適型 | 100 | 150 | z |
| 標準型 | 300 | 450 | 600 |
 .記這8輛轎車的得分的平均數為
.記這8輛轎車的得分的平均數為 ,定義事件
,定義事件 {
{ ,且函數
,且函數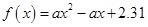 沒有零點},求事件
沒有零點},求事件 發生的概率.
發生的概率. (1)400;(2)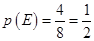 .
.
解析試題分析:(1)設該廠本月生產轎車為 輛,由題意得
輛,由題意得 ,從而得到
,從而得到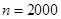 . 計算得到
. 計算得到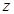 =400;
=400;
(2) 8輛轎車的得分的平均數為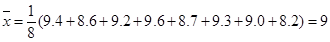
把8輛轎車的得分看作一個總體,從中任取一個分數 對應的基本事件的總數為
對應的基本事件的總數為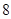 個,
個,
由 ,且函數
,且函數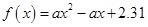 沒有零點建立不等式組求得
沒有零點建立不等式組求得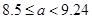 ,進一步得到
,進一步得到 發生當且僅當
發生當且僅當 的值為:8.6,9.2,8.7,9.0共4個,
的值為:8.6,9.2,8.7,9.0共4個,
由古典概型概率的計算公式即得解.
試題解析: (1)設該廠本月生產轎車為 輛,由題意得:
輛,由題意得: ,所以
,所以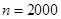 .
. 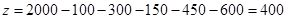 4分
4分
(2) 8輛轎車的得分的平均數為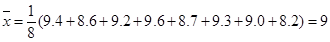 6分
6分
把8輛轎車的得分看作一個總體,從中任取一個分數 對應的基本事件的總數為
對應的基本事件的總數為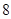 個,
個,
由 ,且函數
,且函數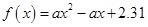 沒有零點
沒有零點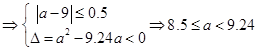 10分
10分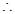
 發生當且僅當
發生當且僅當 的值為:
的值為: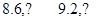 共4個,
共4個,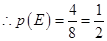 12分
12分
考點:分層抽樣,函數零點,絕對值不等式解法,古典概型.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:解答題
甲、乙、丙三個車床加工的零件分別為350個,700個,1050個,現用分層抽樣的方法隨機抽取6個零件進行檢驗.
(1)從抽取的6個零件中任意取出2個,已知這兩個零件都不是甲車床加工的,求其中至少有一個是乙車床加工的零件;
(2)從抽取的6個零件中任意取出3個,記其中是乙車床加工的件數為X,求X的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了倡導健康、低碳、綠色的生活理念,某市建立了公共自行車服務系統鼓勵市民租用公共自行車出行,公共自行車按每車每次的租用時間進行收費,具體收費標準如下:
①租用時間不超過1小時,免費;
②租用時間為1小時以上且不超過2小時,收費1元;
③租用時間為2小時以上且不超過3小時,收費2元;
④租用時間超過3小時的時段,按每小時2元收費(不足1小時的部分按1小時計算)
已知甲、乙兩人獨立出行,各租用公共自行車一次,兩人租車時間都不會超過3小時,設甲、乙租用時間不超過1小時的概率分別是0.4和0.5;租用時間為1小時以上且不超過2小時的概率分別是0.5和0.3.
(1)求甲、乙兩人所付租車費相同的概率;
(2)設甲、乙兩人所付租車費之和為隨機變量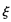 ,求
,求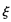 的分布列和數學期望E
的分布列和數學期望E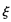 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙、丙三人參加某次招聘會,假設甲能被聘用的概率是 ,甲、丙兩人同時不能被聘用的概率是
,甲、丙兩人同時不能被聘用的概率是 ,乙、丙兩人同時能被聘用的概率為
,乙、丙兩人同時能被聘用的概率為 ,且三人各自能否被聘用相互獨立.
,且三人各自能否被聘用相互獨立.
(1)求乙、丙兩人各自被聘用的概率;
(2)設 為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求
為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求 的分布列與均值(數學期望).
的分布列與均值(數學期望).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
學校游園活動有這樣一個游戲項目:甲箱子里裝有3個白球,2個黑球,乙箱子里裝有1個白球,2個黑球,這些球除顏色外完全相同.每次游戲從這兩個箱子里各隨機摸出2個球,若摸出的白球不少于2個,則獲獎(每次游戲結束后將球放回原箱)
(1)求在一次游戲中
①摸出3個白球的概率;②獲獎的概率.
(2)求在兩次游戲中獲獎次數X的分布列及數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解某班學生喜愛打籃球是否與性別有關,對本班48人進行了問卷調查得到了如下的2×2列聯表:
| | 喜愛打籃球 | 不喜愛打籃球 | 合計 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合計 | | | 48 |
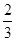 .
.| P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=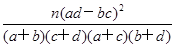 ,其中n=a+b+c+d)
,其中n=a+b+c+d)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
根據以往的成績記錄,甲、乙兩名隊員射擊擊中目標靶的環數的頻率分布情況如圖所示.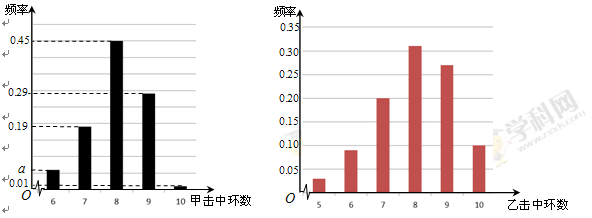
假設每名隊員每次射擊相互獨立.
(Ⅰ)求上圖中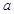 的值;
的值;
(Ⅱ)隊員甲進行三次射擊,求擊中目標靶的環數不低于8環的次數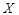 的分布列及數學期望(頻率當作概率使用);
的分布列及數學期望(頻率當作概率使用);
(Ⅲ)由上圖判斷,在甲、乙兩名隊員中,哪一名隊員的射擊成績更穩定?(結論不需證明)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩人進行投籃比賽,兩人各投3球,誰投進的球數多誰獲勝,已知每次投籃甲投進的概率為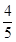 ,乙投進的概率為
,乙投進的概率為 ,求:
,求:
(1)甲投進2球且乙投進1球的概率;
(2)在甲第一次投籃未投進的條件下,甲最終獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某商場為吸引顧客消費推出一項促銷活動,促銷規則如下:到該商場購物消費滿100元就可轉動如圖所示的轉盤一次,進行抽獎(轉盤為十二等分的圓盤),滿200元轉兩次,以此類推;在轉動過程中,假定指針停在轉盤的任一位置都是等可能的;若轉盤的指針落在A區域,則顧客中一等獎,獲得10元獎金;若轉盤落在B區域或C區域,則顧客中二等獎,獲得5元獎金;若轉盤指針落在其他區域,則不中獎(若指針停到兩區間的實線處,則重新轉動).若顧客在一次消費中多次中獎,則對其獎勵進行累加.已知顧客甲到該商場購物消費了268元,并按照規則參與了促銷活動.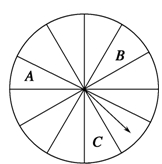
(1)求顧客甲中一等獎的概率;
(2)記X為顧客甲所得的獎金數,求X的分布列及其數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com