
某高校在202年自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組:第1組[75,80),第2組[80,85), 第3組[85,90),第4組[90,95),第5組[95,100]得到的頻率分布直方圖如圖所示.
(1)分別求第3,4,5組的頻率;
(2)若該校決定在筆試成績高的第3,4,5組中用分層抽樣抽取6名學生進入第二輪面試,
(ⅰ)已知學生甲和學生乙的成績均在第三組,求學生甲和學生乙同時進入第二輪面試的概率;
(ⅱ)學校決定在這6名學生中隨機抽取2名學生接受考官D的面試,設第4組中有 名學生被考官D面試,求
名學生被考官D面試,求 的分布列和數學期望.
的分布列和數學期望.
(1)第3,4,5組的頻率分別為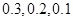 ;(2)學生甲和學生乙同時進入第二輪面試的概率
;(2)學生甲和學生乙同時進入第二輪面試的概率 ;
; 的分布列:
的分布列:
數學期望
0 1 2 P 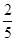

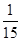
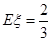 .
.
解析試題分析:(1)根據頻率分步直方圖的性質,根據所給的頻率分步直方圖中小矩形的長和寬,求出矩形的面積,即這組數據的頻率;(2)(ⅰ)本題是一個等可能事件的概率,試驗發生包含的事件數是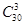 ,滿足條件的事件數是
,滿足條件的事件數是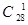 ,根據等可能事件的概率公式,得到結果;(ⅱ)由題意知變量
,根據等可能事件的概率公式,得到結果;(ⅱ)由題意知變量 的可能取值是0,1,2,該變量符合超幾何分布,根據超幾何分布的概率公式寫出變量的概率,寫出這組數據的分布列和期望值.
的可能取值是0,1,2,該變量符合超幾何分布,根據超幾何分布的概率公式寫出變量的概率,寫出這組數據的分布列和期望值.
試題解析:(1) 第三組的頻率為0.06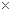 5=0.3;
5=0.3;
第四組的頻率為0.04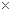 5=0.2;
5=0.2;
第五組的頻率為0.02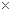 5=0.1. 3分
5=0.1. 3分
(2)(ⅰ)設M:學生甲和學生乙同時進入第二輪面試
P(M)=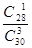 =
= 6分
6分
(ⅱ)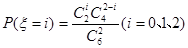 s%5¥u
s%5¥u
10分
0 1 2 P 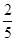

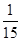
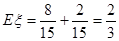 12分
12分
考點:隨機抽樣和樣本估計總體的實際應用;離散型隨機變量的期望與方差.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某籃球運動員在最近幾場大賽中罰球投籃的結果如下:
| 投籃次數n | 8 | 10 | 12 | 9 | 10 | 16 |
| 進球次數m | 6 | 8 | 9 | 7 | 7 | 12 |
| 進球頻率m/n | | | | | | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市職教中心組織廚師技能大賽,大賽依次設基本功(初賽)、面點制作(復賽)、熱菜烹制(決賽)三個輪次的比賽,已知某選手通過初賽、復賽、決賽的概率分別是 ,
, ,
, 且各輪次通過與否相互獨立.
且各輪次通過與否相互獨立.
(1)設該選手參賽的輪次為ξ,求ξ的分布列.
(2)對于(1)中的ξ,設“函數f(x)=3sin π(x∈R)是偶函數”為事件D,求事件D發生的概率.
π(x∈R)是偶函數”為事件D,求事件D發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 年
年 月“神舟 ”發射成功.這次發射過程共有四個值得關注的環節,即發射、實驗、授課、返回.據統計,由于時間關系,某班每位同學收看這四個環節的直播的概率分別為
月“神舟 ”發射成功.這次發射過程共有四個值得關注的環節,即發射、實驗、授課、返回.據統計,由于時間關系,某班每位同學收看這四個環節的直播的概率分別為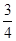 、
、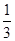 、
、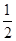 、
、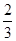 ,并且各個環節的直播收看互不影響.
,并且各個環節的直播收看互不影響.
(1)現有該班甲、乙、丙三名同學,求這 名同學至少有
名同學至少有 名同學收看發射直播的概率;
名同學收看發射直播的概率;
(2)若用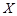 表示該班某一位同學收看的環節數,求
表示該班某一位同學收看的環節數,求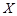 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙、丙三人參加某次招聘會,假設甲能被聘用的概率是 ,甲、丙兩人同時不能被聘用的概率是
,甲、丙兩人同時不能被聘用的概率是 ,乙、丙兩人同時能被聘用的概率為
,乙、丙兩人同時能被聘用的概率為 ,且三人各自能否被聘用相互獨立.
,且三人各自能否被聘用相互獨立.
(1)求乙、丙兩人各自被聘用的概率;
(2)設 為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求
為甲、乙、丙三人中能被聘用的人數與不能被聘用的人數之差的絕對值,求 的分布列與均值(數學期望).
的分布列與均值(數學期望).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設A,B是治療同一種疾病的兩種藥,用若干試驗組進行對比試驗.每個試驗組由4只小白鼠組成,其中2只服用A,另2只服用B,然后觀察療效.若在一個試驗組中,服用A有效的小白鼠的只數比服用B有效的只數多,就稱該試驗組為甲類組.設每只小白鼠服用A有效的概率為 ,服用B有效的概率為
,服用B有效的概率為 .
.
(1)求一個試驗組為甲類組的概率;
(2)觀察三個試驗組,用X表示這三個試驗組中甲類組的個數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
學校游園活動有這樣一個游戲項目:甲箱子里裝有3個白球,2個黑球,乙箱子里裝有1個白球,2個黑球,這些球除顏色外完全相同.每次游戲從這兩個箱子里各隨機摸出2個球,若摸出的白球不少于2個,則獲獎(每次游戲結束后將球放回原箱)
(1)求在一次游戲中
①摸出3個白球的概率;②獲獎的概率.
(2)求在兩次游戲中獲獎次數X的分布列及數學期望E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在打靶訓練中,某戰士射擊一次的成績在9環(包括9環)以上的概率是0.18,在8~9環(包括8環)的概率是0.51,在7~8環(包括7環)的概率是0.15,在6~7環(包括6環)的概率是0.09.計算該戰士在打靶訓練中射擊一次取得8環(包括8環)以上成績的概率和該戰士打靶及格(及格指6環以上包括6環)的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
以下莖葉圖記錄了甲、乙兩組各三名同學在期末考試中的數學成績.乙組記錄中有一個數字模糊,無法確認,假設這個數字具有隨機性,并在圖中以 表示.
表示.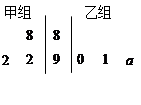
(Ⅰ)若甲、乙兩個小組的數學平均成績相同,求 的值;
的值;
(Ⅱ)求乙組平均成績超過甲組平均成績的概率;
(Ⅲ)當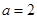 時,分別從甲、乙兩組中各隨機選取一名同學,記這兩名同學數學成績之差的絕對值為
時,分別從甲、乙兩組中各隨機選取一名同學,記這兩名同學數學成績之差的絕對值為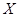 ,求隨機變量
,求隨機變量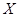 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com