
分析 根據(jù)題意求出f(x)的解析式,再判斷出函數(shù)的單調(diào)性,即可得到答案.
解答 解:由a⊙b=$\left\{\begin{array}{l}{b,a≥b}\\{a,a<b}\end{array}\right.$,
得,f(x)=x?(2-x)=$\left\{\begin{array}{l}{2-x,x≥1}\\{x,x<1}\end{array}\right.$,
∴f(x)在(-∞,1)上是增函數(shù),在[1,+∞)上是減函數(shù),
∴f(x)≤1,
故答案為:1.
點(diǎn)評 本題考查分段函數(shù)的值域,即每段值域的并集,也是一個(gè)新定義運(yùn)算問題:取兩者中較小的一個(gè),求出函數(shù)的解析式并判斷出其單調(diào)性是解題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
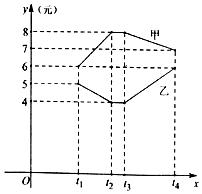 甲乙兩種商品在過去一段時(shí)間內(nèi)的價(jià)格走勢如圖所示,假設(shè)某人持有資金120萬元,他可以在t1至t4的任意時(shí)刻買賣這兩種商品,且買賣能夠立即成交(其他費(fèi)用忽略不計(jì)),那么他持有的資金最多可變?yōu)椋ā 。?table class="qanwser">
甲乙兩種商品在過去一段時(shí)間內(nèi)的價(jià)格走勢如圖所示,假設(shè)某人持有資金120萬元,他可以在t1至t4的任意時(shí)刻買賣這兩種商品,且買賣能夠立即成交(其他費(fèi)用忽略不計(jì)),那么他持有的資金最多可變?yōu)椋ā 。?table class="qanwser">查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $-\frac{7}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | k1<k2<k3 | B. | k2<k1<k3 | C. | k3<k2<k1 | D. | k1<k3<k2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | $\frac{2015}{672}$ | D. | $\frac{2015}{336}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com