
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 由題意:三棱錐ABCD的棱長都相等,可知該幾何體是正三棱錐.題目要求解的是兩條異面直線所成角的余弦值,且給出了棱AB的中點E,可以想到再找AD的中點F,連接兩中點EF,得到EF∥BD,則直線CE與直線BD所成角轉化為直線CE與直線EF所成角,在三角形CEF中運用余弦定理可求∠CEF的余弦值,則直線CE與直線BD所成角的余弦值可求.
解答 解:如圖,取AD中點F,連接EF,因為E、F分別為AB、AD的中點,
則EF為三角形ABD的中位線,所以EF∥BD,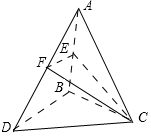 所以直線EF與CE所成的角即為直線CE與直線BD所成角,
所以直線EF與CE所成的角即為直線CE與直線BD所成角,
因為三棱錐A-BCD的棱長全相等,設棱長為2a,則EF=a,
在等邊三角形ABC中,因為F為AD的中點,所以CF為邊AD上的高,
所以CF=$\sqrt{A{C}^{2}-A{F}^{2}}=\sqrt{4{a}^{2}-{a}^{2}}=\sqrt{3}a$
同理∴CF=CE=$\sqrt{3}a$
在三角形CEF中:cos∠CEF=$\frac{F{E}^{2}+C{E}^{2}-C{F}^{2}}{2FE•CE}$=$\frac{\sqrt{3}}{6}$.
所以,直線CE與直線BD所成角的余弦值為$\frac{\sqrt{3}}{6}$.
故選B.
點評 本題考查空間點、線、面的位置關系及學生的空間想象能力、求異面直線角的能力.在立體幾何中找平行線是解決問題的一個重要技巧,這個技巧就是通過三角形的中位線找平行線,如果試題的已知中涉及到多個中點,則找中點是出現平行線的關鍵技巧,此題是中低檔題.


科目:高中數學 來源: 題型:解答題
 已知函數f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),x∈(-1,1)\\-{x^2}+4x-4,x∈[1,+∞)\end{array}$
已知函數f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),x∈(-1,1)\\-{x^2}+4x-4,x∈[1,+∞)\end{array}$查看答案和解析>>
科目:高中數學 來源: 題型:解答題
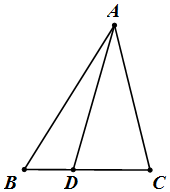 在△ABC中,D為BC邊上的動點,且AD=3,B=$\frac{π}{3}$.
在△ABC中,D為BC邊上的動點,且AD=3,B=$\frac{π}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
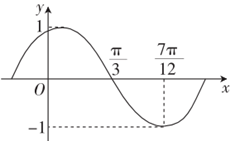 已知函數f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$),其導函數f'(x)的部分圖象如圖所示,則函數f(x)的解析式為( )
已知函數f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<$\frac{π}{2}$),其導函數f'(x)的部分圖象如圖所示,則函數f(x)的解析式為( )| A. | $f(x)=cos(2x-\frac{π}{6})$ | B. | $f(x)=sin(2x+\frac{π}{6})$ | C. | $f(x)=\frac{1}{2}cos(2x+\frac{π}{6})$ | D. | $f(x)=\frac{1}{2}sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {0,-1} | B. | {-2,-1} | C. | {-2,2} | D. | {0,2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{19}{25}$ | B. | $\frac{25}{36}$ | C. | $\frac{31}{48}$ | D. | $\frac{49}{64}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com