
分析 (Ⅰ)先化簡f(x),再根據正弦函數的圖象和性質即可求出函數f(x)的單調遞增區間及其對稱中心,
(Ⅱ)先求出A,再根據向量的加減的幾何意義和向量的數量積公式,以及三角形的面積公式計算即可.
解答 解:(Ⅰ)f(x)=2$\sqrt{3}$sin2($\frac{π}{4}$+x)+2sin($\frac{π}{4}$+x)cos($\frac{π}{4}$+x)=$\sqrt{3}$[1-cos($\frac{π}{2}$+2x)]+sin($\frac{π}{2}$+2x)=$\sqrt{3}$sin2x+cos2x+$\sqrt{3}$=2sin(2x+$\frac{π}{6}$)+$\sqrt{3}$,
由-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,
解得-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,
∴函數f(x)的單調遞增區間為[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z,
令2x+$\frac{π}{6}$=kπ,解得x=-$\frac{π}{12}$+$\frac{kπ}{2}$,
則對稱中心為(-$\frac{π}{12}$+$\frac{kπ}{2}$,$\sqrt{3}$),k∈Z;
(Ⅱ)f(A)=$\sqrt{3}$+1,
∴2sin(2A+$\frac{π}{6}$)+$\sqrt{3}$=$\sqrt{3}$+1,
∴sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,
解得A=$\frac{π}{3}$,
∵|$\overrightarrow{BC}$|=|$\overrightarrow{AC}$-$\overrightarrow{AB}$|=3,①,
BC邊上的中線為3,則|$\overrightarrow{AC}$+$\overrightarrow{AB}$|=6,②,
由①②知$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{27}{4}$,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|•cos$\frac{π}{3}$=$\frac{27}{4}$,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=$\frac{27}{2}$,
∴S=$\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|sin$\frac{π}{3}$=$\frac{27\sqrt{3}}{8}$.
點評 本題考查了三角函數的化簡以及正弦函數的圖象和性質,向量的加減的幾何意義和向量的數量積公式,以及三角形的面積公式,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,4) | B. | (0,4) | C. | {0,1,2,3} | D. | {1,2,3} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
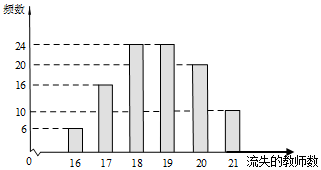 2017年兩會繼續關注了鄉村教師的問題,隨著城鄉發展失衡,鄉村教師待遇得不到保障,流失現象嚴重,教師短缺會嚴重影響鄉村孩子的教育問題,為此,某市今年要為某所鄉村中學招聘儲備未來三年的教師,現在每招聘一名教師需要2萬元,若三年后教師嚴重短缺時再招聘,由于各種因素,則每招聘一名教師需要5萬元,已知現在該鄉村中學無多余教師,為決策應招聘多少鄉村教師搜集并整理了該市100所鄉村中學在過去三年內的教師流失數,得到右面的柱狀圖:記x表示一所鄉村中學在過去三年內流失的教師數,y表示一所鄉村中學未來四年內在招聘教師上所需的費用(單位:萬元),n表示今年為該鄉村中學招聘的教師數,為保障鄉村孩子教育不受影響,若未來三年內教師有短缺,則第四年馬上招聘
2017年兩會繼續關注了鄉村教師的問題,隨著城鄉發展失衡,鄉村教師待遇得不到保障,流失現象嚴重,教師短缺會嚴重影響鄉村孩子的教育問題,為此,某市今年要為某所鄉村中學招聘儲備未來三年的教師,現在每招聘一名教師需要2萬元,若三年后教師嚴重短缺時再招聘,由于各種因素,則每招聘一名教師需要5萬元,已知現在該鄉村中學無多余教師,為決策應招聘多少鄉村教師搜集并整理了該市100所鄉村中學在過去三年內的教師流失數,得到右面的柱狀圖:記x表示一所鄉村中學在過去三年內流失的教師數,y表示一所鄉村中學未來四年內在招聘教師上所需的費用(單位:萬元),n表示今年為該鄉村中學招聘的教師數,為保障鄉村孩子教育不受影響,若未來三年內教師有短缺,則第四年馬上招聘查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|0<x<1} | B. | {x|-1≤x≤2} | C. | {x|-1<x<2} | D. | {x|0≤x≤1} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com