
若a、b、c都是正數,且至少有一個不為1,axbycz=aybzcx=azbxcy=1,則x、y、z應滿足的關系是________.
解:由axbycz=1,兩邊取對數,得xlg a+ylg b+zlg c=0,
同理ylg a+zlg b+xlg c=0,zlg a+xlg b+ylg c=0.
三式相加,得(x+y+z)lg a+(x+y+z)lg b+(x+y+z)lg c=0.
∴(x+y+z)(1g a+lg b+lg c)=0.∴x+y+z=0,或lg a+lg b+lg c=0.
由lg a+lg b+lg c=0,得lg abc=0,
abc=1,a=![]() ,
,
將①代入axbycz=1,得by-xcz-x=1,
又a、b、c不全為1,只有當y-x=z-x=0.
即x=y=z時,等式成立.
∴填x+y+z=0或x=y=z.


科目:高中數學 來源:2012-2013學年浙江省臺州中學高二(下)期中數學試卷(理科)(解析版) 題型:選擇題
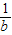 ,b+
,b+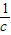 ,c+
,c+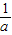 三數中至少有一個不小于2”,提出的假設是( )
三數中至少有一個不小于2”,提出的假設是( )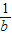 ,b+
,b+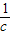 ,c+
,c+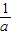 至少有一個小于2
至少有一個小于2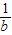 ,b
,b ,c+
,c+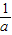 都小于2
都小于2查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com