
分析 (1)首先對f(x)求導,利用導數判斷函數的單調性與函數最值即可;
(2)當b>0時,即導函數零點:x=$\frac{1}{b}$;所以f(x)在(0,$\frac{1}{b}$)上單調遞減,在($\frac{1}{b}$,+∞)上單調遞增;
再分類討論$\frac{1}{b}$與e的關系;
解答 解:(1)由題意,f(x)=-x2+3x-lnx,定義域為:x>0
對f(x)求導:f'(x)=-2x+3-$\frac{1}{x}$,令f'(x)=0,則有x1=$\frac{1}{2}$,x2=1;
當x∈(0,$\frac{1}{2}$)時,f'(x)<0,則f(x)在(0,$\frac{1}{2}$)上單調遞減;
當x∈($\frac{1}{2}$,1)時,f'(x)>0,則f(x)在($\frac{1}{2}$,1)上單調遞增;
當x∈(1,+∞)時,f'(x)<0,則f(x)在(1,+∞)上單調遞減;
所以f(x)max=f(1)=2,f(x)min={f($\frac{1}{2}$),f(2)}=f($\frac{1}{2}$)=ln2+$\frac{5}{4}$;
(2)當a=0時,f(x)=bx-lnx (x>0)
對f(x)求導,即f'(x)=b-$\frac{1}{x}$
當b>0時,令f'(x)=0,即導函數零點:x=$\frac{1}{b}$;
所以f(x)在(0,$\frac{1}{b}$)上單調遞減,在($\frac{1}{b}$,+∞)上單調遞增;
(i)當$\frac{1}{b}$>e時,即:b<$\frac{1}{e}$,f(x)在(0,e]上單調遞減,此時最小值為f(e).
由題意,f(e)=3,即:b=$\frac{3}{e}$,不合題意;
(ii)當$\frac{1}{b}$≤e時,即:b≥$\frac{1}{e}$,f(x)在(0,$\frac{1}{b}$)上遞減,在($\frac{1}{b}$,e)上遞增;
此時最小值為f(b).
由題意:f(b)=3,即:b=e2,滿足題意.
綜上:b=e2.
點評 本題主要考查了利用導數判斷函數的單調性,求函數最值以及分類討論思想的應用,屬中等題.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,+∞) | B. | (1,+∞) | C. | [1,3)∪(3,+∞) | D. | (1,3)∪(3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知函數f(x)=x2-2|x|-3.
已知函數f(x)=x2-2|x|-3.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=±2$\sqrt{2}$x | B. | y=±2$\sqrt{6}$x | C. | y=±5x | D. | y=±$\frac{3}{4}$x |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
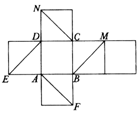 如圖是正方體的平面展開圖,則在這個正方體中,以下四個判斷中,正確的序號是②④.
如圖是正方體的平面展開圖,則在這個正方體中,以下四個判斷中,正確的序號是②④.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com