【題目】已兩動圓
和
，把它們的公共點的軌跡記為曲線
，若曲線與
軸的正半軸交點為
，且曲線上異于點的相異兩點
、
滿足
.
(1)求曲線的方程；
(2)證明直線
恒經過一定點，并求出此定點的坐標.
【答案】（1）
；（2）直線
恒過定點
。
【解析】
（1）設兩動圓的公共點為
，則有
，運用橢圓的定義，即可得到
，
，
，進而得到的軌跡方程；
（2）
，設
，
，
，
，根據直線的斜率不存在和存在，設出直線方程，根據條件，運用向量的數量積的坐標表示，結合韋達定理和直線恒過定點的求法，即可得到定點；
解：（1）設兩動圓的公共點為，則有
．
由橢圓的定義可知的軌跡是以
、
為焦點橢圓，且
．
，
所以曲線
的方程是：．
（2）證明：由題意可知：，設，，，，
當的斜率不存在時，易知滿足條件
的直線為：
，過定點；
當的斜率存在時，設直線
，聯立方程組：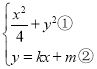
，
把②代入①有：
，
③，
④，
因為，所以有
即
，
，
把③④代入整理：
，
（有公因式
繼續化簡得
，
或
（舍去
，
綜上，直線恒過定點．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】已知拋物線
與橢圓
有一個相同的焦點，過點
且與
軸不垂直的直線
與拋物線
交于
，
兩點，關于軸的對稱點為
.
（1）求拋物線的方程；
（2）試問直線
是否過定點？若是，求出該定點的坐標；若不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若四面體
的三組對棱分別相等，即
，給出下列結論：
①四面體每組對棱相互垂直；
②四面體每個面的面積相等；
③從四面體每個頂點出發的三條棱兩兩夾角之和大
而小于
；
④連接四面體每組對棱中點的線段相互垂直平分.
其中正確結論的序號是__________． (寫出所有正確結論的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
央視春晚長春分會場，演員身穿獨特且輕薄的石墨烯發熱服，在寒氣逼人的零下
春晚現場表演了精彩的節目.石墨烯發熱服的制作：從石墨中分離出石墨烯，制成石墨烯發熱膜，再把石墨烯發熱膜鋪到衣服內.
（1）從石墨分離石墨烯的一種方法是化學氣相沉積法，使石墨升華后附著在材料上再結晶。現在有
材料、
材料供選擇，研究人員對附著在材料上再結晶做了
次試驗，成功
次；對附著在材料上再結晶做了次試驗，成功
次.用二列聯表判斷：是否有
的把握認為試驗是否成功與材料和材料的選擇有關？
|
| |
成功 | ||
不成功 |
（2）研究人員得到石墨烯后，再制作石墨烯發熱膜有四個環節：①透明基底及
膠層；②石墨烯層；③銀漿線路；④表面封裝層。前三個環節每個環節生產合格的概率為
，每個環節不合格需要修復的費用均為
元；第四環節生產合格的概率為
元，問：一次生產出來的石墨烯發熱膜成為合格品平均需要多少修復費用？
附：
，其中
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列4個命題，其中正確命題的序號____________.
①
；
②函數
有
個零點；
③函數
的圖象關于點
對稱。
④已知
，函數
的圖象過點
，則
的最小值是
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4－4：坐標系與參數方程(本題滿分10分)
在平面直角坐標系中，將曲線
向左平移2個單位，再將得到的曲線上的每一個點的橫坐標保持不變，縱坐標縮短為原來的
，得到曲線
，以坐標原點
為極點，
軸的正半軸為極軸，建立極坐標系，的極坐標方程為
．
（1）求曲線的參數方程；
（2）已知點
在第一象限，四邊形
是曲線的內接矩形，求內接矩形周長的最大值，并求周長最大時點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱
中，
，點
分別為棱
的中點．
（Ⅰ）求證：
∥平面
(Ⅱ)求證：平面
平面;
(Ⅲ)在線段
上是否存在一點
，使得直線
與平面
所成的角為300?如果存在，求出線段
的長；如果不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
上兩點
、
，焦點
滿足
，線段
的垂直平分線過
.
（1）求拋物線
的方程；
（2）過點作直線
，使得拋物線上恰有三個點到直線的距離都為
，求直線的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
