
分析 由向量的平方即為模的平方,化簡整理可得x2$\overrightarrow{a}$2+2x$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2≥0恒成立,可得4($\overrightarrow{a}$•$\overrightarrow{b}$)2-4$\overrightarrow{a}$2•($\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2)≤0,(θ為$\overrightarrow{a}$,$\overrightarrow{b}$的夾角),即有(cosθ-$\frac{1}{2}$)2≤0,可得cosθ=$\frac{1}{2}$,sinθ=$\frac{\sqrt{3}}{2}$,可設(shè)|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,設(shè)$\overrightarrow{OA}$=$\overrightarrow{a}$=(2,0),$\overrightarrow{OB}$=$\overrightarrow{b}$=(1,$\sqrt{3}$),$\overrightarrow{OC}$=$\overrightarrow{c}$,C在單位圓上運(yùn)動,由$\overrightarrow{OP}$=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$可得P在線段AB上運(yùn)動(不含端點(diǎn)),求出AB的方程,運(yùn)用點(diǎn)到直線的距離公式可得O到AB的距離,即可得到所求最值和范圍.
解答  解:對任意的x∈R,都有|$\overrightarrow{b}$+x$\overrightarrow{a}$|≥|$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$|,
解:對任意的x∈R,都有|$\overrightarrow{b}$+x$\overrightarrow{a}$|≥|$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$|,
即有($\overrightarrow{b}$+x$\overrightarrow{a}$)2≥($\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$)2,
即為$\overrightarrow{b}$2+2x$\overrightarrow{a}$•$\overrightarrow{b}$+x2$\overrightarrow{a}$2≥$\overrightarrow{b}$2-$\overrightarrow{a}$•$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{a}$2,
由|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,可得x2$\overrightarrow{a}$2+2x$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2≥0恒成立,
可得4($\overrightarrow{a}$•$\overrightarrow{b}$)2-4$\overrightarrow{a}$2•($\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$2)≤0,(θ為$\overrightarrow{a}$,$\overrightarrow{b}$的夾角),
即為|$\overrightarrow{a}$|4•cos2θ-|$\overrightarrow{a}$|4•cosθ+$\frac{1}{4}$|$\overrightarrow{a}$|4≤0,
即有(cosθ-$\frac{1}{2}$)2≤0,(cosθ-$\frac{1}{2}$)2≥0,
可得cosθ=$\frac{1}{2}$,sinθ=$\frac{\sqrt{3}}{2}$,
可設(shè)|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=1,
設(shè)$\overrightarrow{OA}$=$\overrightarrow{a}$=(2,0),$\overrightarrow{OB}$=$\overrightarrow{b}$=(1,$\sqrt{3}$),
$\overrightarrow{OC}$=$\overrightarrow{c}$,C在單位圓上運(yùn)動,
由$\overrightarrow{OP}$=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$可得P在線段AB上運(yùn)動(不含端點(diǎn)),
直線AB的方程為y-0=-$\sqrt{3}$(x-2),
即為$\sqrt{3}$x+y-2$\sqrt{3}$=0.
由原點(diǎn)到直線AB的距離為$\frac{|0+0-2\sqrt{3}|}{\sqrt{3+1}}$=$\sqrt{3}$,
即有單位圓上的點(diǎn)到線段AB的距離的最小值為$\sqrt{3}$-1,最大值為$\sqrt{3}$+1,
則$\frac{|\overrightarrow{c}-λ\overrightarrow{a}-(1-λ)\overrightarrow{b}|}{|\overrightarrow{a}|}$=$\frac{|\overrightarrow{OC}-\overrightarrow{OP}|}{2}$的范圍是[$\frac{1}{2}$($\sqrt{3}$-1),$\frac{1}{2}$($\sqrt{3}$+1)].
故答案為:[$\frac{1}{2}$($\sqrt{3}$-1),$\frac{1}{2}$($\sqrt{3}$+1)].
點(diǎn)評 本題考查向量數(shù)量積的運(yùn)用,注意運(yùn)用性質(zhì):向量的平方即為模的平方,考查恒成立思想轉(zhuǎn)化為二次不等式恒成立問題的解法,以及數(shù)形結(jié)合的思想方法,考查化簡整理的運(yùn)算能力,屬于難題.


 世紀(jì)百通主體課堂小學(xué)課時同步達(dá)標(biāo)系列答案
世紀(jì)百通主體課堂小學(xué)課時同步達(dá)標(biāo)系列答案 世紀(jì)百通優(yōu)練測系列答案
世紀(jì)百通優(yōu)練測系列答案 百分學(xué)生作業(yè)本題練王系列答案
百分學(xué)生作業(yè)本題練王系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
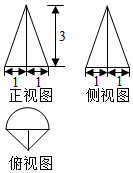 某幾何體的三視圖如圖所示(單位:cm),則該幾何體的體積(單位:cm2)是( )
某幾何體的三視圖如圖所示(單位:cm),則該幾何體的體積(單位:cm2)是( )| A. | $\frac{π}{2}$+1 | B. | $\frac{π}{2}$+3 | C. | $\frac{3π}{2}$+1 | D. | $\frac{3π}{2}$+3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
| 1 | 2 | 3 | … | m+n |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com