
【題目】已知函數![]() ,
,![]() ,若對任意給定的
,若對任意給定的![]() ,關于
,關于![]() 的方程
的方程![]() 在區間
在區間![]() 上總存在唯一的一個解,則實數
上總存在唯一的一個解,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:由題意可以把問題轉化為求函數f(x)和函數g(x)的值域,并有題意轉化為兩個函數的值域的關系問題.
詳解:解f′(x)=6ax2﹣6ax=6ax(x﹣1),
①當a=0時,f(x)=1,g(x)=![]() ,顯然不可能滿足題意;
,顯然不可能滿足題意;
②當a>0時,f'(x)=6ax2﹣6ax=6ax(x﹣1),
x,f′(x),f(x)的變化如下:

又因為當a>0時,g(x)=﹣![]() x+
x+![]() 上是減函數,
上是減函數,
對任意m∈[0,2],g(m)∈[﹣![]() +
+![]() ,
,![]() ],
],
由題意,必有g(m)max≤f(x)max,且1﹣a>0,
故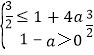 ,解得:
,解得:![]() ≤a<1,
≤a<1,
③當a<0時,g(x)=﹣![]() x+
x+![]() 上是增函數,不合題意;
上是增函數,不合題意;
綜上,a∈[![]() ,1),
,1),
故選:B.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數.
為奇函數.
(1)求![]() 的值,并求
的值,并求![]() 的定義域;
的定義域;
(2)判斷函數![]() 的單調性,不需要證明;
的單調性,不需要證明;
(3)若對于任意![]() ,是否存在實數
,是否存在實數![]() ,使得不等式
,使得不等式![]() 恒成立?若存在,求出實數
恒成立?若存在,求出實數![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() 且與
且與![]() 軸相切,點
軸相切,點![]() 關于圓心
關于圓心![]() 的對稱點為
的對稱點為![]() ,動點
,動點![]() 的軌跡記為
的軌跡記為![]() .
.
(1)求![]() 的方程;
的方程;
(2)設直線![]() :
:![]() 與曲線
與曲線![]() 交于點
交于點![]() 、
、![]() ;直線
;直線![]() :
:![]() 與
與![]() 交于點
交于點![]() ,
,![]() ,其中
,其中![]() ,以
,以![]() 、
、![]() 為直徑的圓
為直徑的圓![]() 、
、![]() (
(![]() 、
、![]() 為圓心)的公共弦所在直線記為
為圓心)的公共弦所在直線記為![]() ,求
,求![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有A、B兩種型號臺燈,若購買2臺A型臺燈和6臺B型臺燈共需610元,若購買6臺A型臺燈和2臺B型臺燈共需470元.
(1)求A、B兩種型號臺燈每臺分別多少元?
(2)采購員小紅想采購A、B兩種型號臺燈共30臺,且總費用不超過2200元,則最多能采購B型臺燈多少臺?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中嘗試進行課堂改革.現高一有![]() 兩個成績相當的班級,其中
兩個成績相當的班級,其中![]() 班級參與改革,
班級參與改革,![]() 班級沒有參與改革.經過一段時間,對學生學習效果進行檢測,規定成績提高超過
班級沒有參與改革.經過一段時間,對學生學習效果進行檢測,規定成績提高超過![]() 分的為進步明顯,得到如下列聯表.
分的為進步明顯,得到如下列聯表.
進步明顯 | 進步不明顯 | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
(1)是否有![]() 的把握認為成績進步是否明顯與課堂是否改革有關?
的把握認為成績進步是否明顯與課堂是否改革有關?
(2)按照分層抽樣的方式從![]() 班中進步明顯的學生中抽取
班中進步明顯的學生中抽取![]() 人做進一步調查,然后從
人做進一步調查,然后從![]() 人中抽
人中抽![]() 人進行座談,求這
人進行座談,求這![]() 人來自不同班級的概率.
人來自不同班級的概率.
附: ,當
,當![]() 時,有
時,有![]() 的把握說事件
的把握說事件![]() 與
與![]() 有關.
有關.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() (
(![]() 為常數,且
為常數,且![]() ).
).
(1)若當![]() 時,函數
時,函數![]() 與
與![]() 的圖象有且只要一個交點,試確定自然數
的圖象有且只要一個交點,試確定自然數![]() 的值,使得
的值,使得![]() (參考數值
(參考數值![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)當![]() 時,證明:
時,證明:![]() (其中
(其中![]() 為自然對數的底數).
為自然對數的底數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地擬規劃種植一批芍藥,為了美觀,將種植區域(區域I)設計成半徑為1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).為方便觀賞,增加收入,在種植區域外圍規劃觀賞區(區域II)和休閑區(區域III),并將外圍區域按如圖所示的方案擴建成正方形
).為方便觀賞,增加收入,在種植區域外圍規劃觀賞區(區域II)和休閑區(區域III),并將外圍區域按如圖所示的方案擴建成正方形![]() ,其中點
,其中點![]() ,
,![]() 分別在邊
分別在邊![]() 和
和![]() 上.已知種植區、觀賞區和休閑區每平方千米的年收入分別是10萬元、20萬元、20萬元.
上.已知種植區、觀賞區和休閑區每平方千米的年收入分別是10萬元、20萬元、20萬元.
(1)要使觀賞區的年收入不低于5萬元,求![]() 的最大值;
的最大值;
(2)試問:當![]() 為多少時,年總收入最大?
為多少時,年總收入最大?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com