
【題目】已知動圓![]() 過定點
過定點![]() 且與
且與![]() 軸相切,點
軸相切,點![]() 關于圓心
關于圓心![]() 的對稱點為
的對稱點為![]() ,動點
,動點![]() 的軌跡記為
的軌跡記為![]() .
.
(1)求![]() 的方程;
的方程;
(2)設直線![]() :
:![]() 與曲線
與曲線![]() 交于點
交于點![]() 、
、![]() ;直線
;直線![]() :
:![]() 與
與![]() 交于點
交于點![]() ,
,![]() ,其中
,其中![]() ,以
,以![]() 、
、![]() 為直徑的圓
為直徑的圓![]() 、
、![]() (
(![]() 、
、![]() 為圓心)的公共弦所在直線記為
為圓心)的公共弦所在直線記為![]() ,求
,求![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)設![]() ,則
,則![]() ,結合直線與圓相切的充分必要條件可得
,結合直線與圓相切的充分必要條件可得![]() .整理化簡,則軌跡方程為
.整理化簡,則軌跡方程為![]() .
.
(2)設![]() ,
,![]() ,聯立直線與拋物線的方程可得
,聯立直線與拋物線的方程可得![]() ,
,
![]() ,結合韋達定理可得以
,結合韋達定理可得以![]() 為直徑的圓的方程是:
為直徑的圓的方程是:![]() ,化簡可得
,化簡可得![]() ,同理可得以
,同理可得以![]() 為直徑的圓的方程是:
為直徑的圓的方程是:![]() ,兩式作差可得
,兩式作差可得![]() 的方程是:
的方程是:![]() .結合點到直線距離公式可得
.結合點到直線距離公式可得![]() ,則所求距離最小值為
,則所求距離最小值為![]() .
.
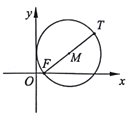
詳解:(1)如圖,設![]() ,則
,則![]() ,
,
由題可知![]() ,動圓
,動圓![]() 與
與![]() 軸相切,得
軸相切,得![]() .
.
即![]() .
.
化簡得:![]() .
.
(2)設![]() ,
,![]() ,
,
將![]() 代入
代入![]() 得:
得:![]() ,
,![]() ,
,
則:![]() ,
,
且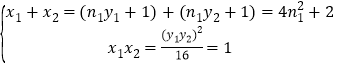 ①
①
設![]() 是
是![]() 上的任意一點.
上的任意一點.
由![]() 得以
得以![]() 為直徑的圓的方程是:
為直徑的圓的方程是:
![]() ,
,
將①式代入上式,化簡得:![]() ②
②
同理以![]() 為直徑的圓的方程是:
為直徑的圓的方程是:![]() ③
③
②![]() ③得
③得![]() 的方程是:
的方程是:![]() .
.
又![]() ,
,
![]() 到
到![]() 的距離:
的距離:![]()
當![]() 時,所求距離最小值為
時,所求距離最小值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】國慶期間,某旅行社組團去風景區旅游,若旅行團人數不超過20人,每人需交費用800元;若旅行團人數超過20人,則給予優惠:每多1人,人均費用減少10元,直到達到規定人數60人為止.旅行社需支付各種費用共計10000元.
(1)寫出每人需交費用S關于旅行團人數![]() 的函數;
的函數;
(2)旅行團人數x為多少時,旅行社可獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)的定義域是(0,+∞),且對任意正實數x,y都有f(xy)=f(x)+f(y)恒成立,已知f(2)=1,且x>1時,f(x)>0.
(1)求f(![]() )的值;
)的值;
(2)判斷y=f(x)在(0,+∞)上的單調性并給出證明;
(3)解不等式f(2x)>f(8x-6)-1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】紅星海水養殖場進行某水產品的新舊養殖方法的產量對比,收貨時在舊養殖的大量網箱中隨機抽取![]() 個網箱,在新養殖法養殖的大量網箱中也隨機抽取
個網箱,在新養殖法養殖的大量網箱中也隨機抽取![]() 個網箱,測量各箱水產品的產量,得樣本頻率分布直方圖如下:
個網箱,測量各箱水產品的產量,得樣本頻率分布直方圖如下:

(1)填寫下列列聯表,并根據列聯表判斷是否有![]() 的把握認為箱產量與養殖方法有關.
的把握認為箱產量與養殖方法有關.
養殖法 箱產量 | 箱產量 | 箱產量 | 總計 |
舊養殖法 | |||
新養殖法 | |||
總計 |
(2)設兩種養殖方法的產量互相獨立,記![]() 表示事件:“舊養殖法的箱產量低于
表示事件:“舊養殖法的箱產量低于![]() ,新養殖法的箱產量不低于
,新養殖法的箱產量不低于![]() ”,估計
”,估計![]() 的概率;
的概率;
(3)某水產批發戶從紅星海水養殖場用新養殖法養殖的大量網箱水產品中購買了![]() 個網箱的水產品,記
個網箱的水產品,記![]() 表示箱產量位于區間
表示箱產量位于區間![]() 的網箱個數,以上樣本在相應區間的頻率代替概率,求
的網箱個數,以上樣本在相應區間的頻率代替概率,求![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近期,某公交公司分別推出支付寶和微信掃碼支付乘車活動,活動設置了一段時間的推廣期,由于推廣期內優惠力度較大,吸引越來越多的人開始使用掃碼支付,某線路公交車隊統計了活動剛推出一周內每一天使用掃碼支付的人次,用x表示活動推出的天數,y表示每天使用掃碼支付的人次(單位:十人次),繪制了如圖所示的散點圖:
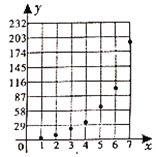
(I)根據散點圖判斷在推廣期內,![]() 與
與![]() (c,d為為大于零的常數)哪一個適宜作為掃碼支付的人次y關于活動推出天數x的回歸方程類型?(給出判斷即可,不必說明理由)
(c,d為為大于零的常數)哪一個適宜作為掃碼支付的人次y關于活動推出天數x的回歸方程類型?(給出判斷即可,不必說明理由)
(Ⅱ)根據(I)的判斷結果求y關于x的回歸方程,并預測活動推出第8天使用掃碼支付的人次.
參考數據:
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: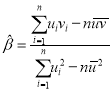 ,
,![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】5名男生4名女生站成一排,求滿足下列條件的排法:
(1)女生都不相鄰有多少種排法?
(2)男生甲、乙、丙排序一定(只考慮位置的前后順序),有多少種排法?
(3)男甲不在首位,男乙不在末位,有多少種排法?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com