
| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
分析 由平均數的定義,計算即可判斷①;
運用平均數、中位數和眾數的定義,即可判斷②;
由線性回歸直線必過樣本中心點,即可判斷③;
由ξ服從正態分布N(0,σ2),即曲線關于y軸對稱,求得P(ξ<-2),即可判斷④.
解答 解:①由題意可得這兩個班的數學平均分為$\frac{ma+nb}{m+n}$,故①錯;
②由題意可得a=$\frac{1}{10}$(15+17+14+10+15+17+17+16+14+12)=14.7,b=15,c=17,
即有c>b>a,故②錯;
③由線性回歸方程的特點,可得回歸直線$\widehaty=\widehatbx+\widehata$必過樣本中心點($\overline x,\overline y$),故③對;
④已知ξ服從正態分布N(0,σ2),且P(-2≤ξ≤0)=0.4,則P(ξ<-2)=0.5-0.4=0.1,
則P(ξ>2)=P(ξ<-2)=0.1,故④錯.
故選:D.
點評 本題考查命題的真假判斷,考查平均數、中位數和眾數,以及線性回歸直線和正態分布的特點,考查判斷能力,屬于基礎題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (3,1) | B. | (-1,3) | C. | (3,-1) | D. | (2,4) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若m?α,n?α,m∥n,則n∥α | |
| B. | 若α⊥γ,α∥β,則β⊥γ | |
| C. | 若m?β,n是l在β內的射影,若m⊥l,則m⊥n | |
| D. | 若α⊥β,α∩β=m,l⊥m,則l⊥β |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
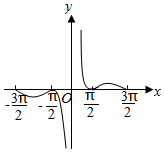 已知函數f(x)的圖象如圖所示,則f(x)的解析式可能是( )
已知函數f(x)的圖象如圖所示,則f(x)的解析式可能是( )| A. | $\frac{|cos3x|}{x}$ | B. | $\frac{1+cos2x}{2x}$ | ||
| C. | $\frac{(4{x}^{2}-{π}^{2})(4{x}^{2}-9{π}^{2})}{{x}^{5}}$ | D. | $\frac{|sin2x|}{x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com