
| MN |
| AB |
| OP |
| OQ |
| OP |
| OQ |
| MN |
| AB |
| x |
| 3 |
| 0+0+x |
| 3 |
| 1-1+y |
| 3 |
| x |
| 3 |
| y |
| 3 |
| MN |
| AB |
| x |
| 3 |
(
|
(
|
| x2 |
| 3 |
| x2 |
| 3 |
| OP |
| OQ |
| 6kb |
| 1+3k2 |
| 3b2-3 |
| 1+3k2 |
| 3b2-3 |
| 1+3k2 |
| 6kb |
| 1+3k2 |
| ||
| 2 |
| ||
| 2 |
| 3b |
| 2 |
| 3b2-3 |
| 4 |
| OP |
| OQ |
| 3b2-3 |
| 4 |
| -3b |
| 2 |
| 3 |
| 2 |
| ||
| 2 |


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:高中數學 來源: 題型:
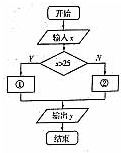 某客運部門規定甲、乙兩地之間旅客托運行李的費用為:不超過25kg按0.5元/kg收費,超過25kg的部分按0.8元/kg收費,計算收費的程序框圖如右圖所示,則①②處應填( )
某客運部門規定甲、乙兩地之間旅客托運行李的費用為:不超過25kg按0.5元/kg收費,超過25kg的部分按0.8元/kg收費,計算收費的程序框圖如右圖所示,則①②處應填( )| A、y=0.8x y=0.5x |
| B、y=0.5x y=0.8x |
| C、y=25×0.5+(x-25)×0.8 y=0.5x |
| D、y=25×0.5+0.8x y=0.8x |
查看答案和解析>>
科目:高中數學 來源: 題型:
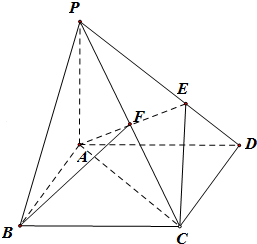 如圖,在四棱錐P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中點,
如圖,在四棱錐P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中點,查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com