
分析 (1)由遞推關系可得:(an+an-1)(an-an-1)=2(an+an-1).an>0,可得an-an-1=2(n≥2),利用等差數列的通項公式即可得出.
(2)利用“裂項求和”方法與數列的單調性即可得出.
解答 解:(1)由${a_n}^2+2{a_n}=4{S_n}+3$,①
可知${a_{n-1}}^2+2{a_{n-1}}=4{S_{n-1}}+3$,②(n≥2)
①-②得:${a_n}^2-{a_{n-1}}^2+2{a_n}-2{a_{n-1}}=4{a_n}$,
即(an+an-1)(an-an-1)=2(an+an-1).
∵an>0,∴an+an-1≠0,
∴an-an-1=2(n≥2),
∴{an}是以a1=3為首項,d=2為公差的等差數列.
∴${a_n}=2n+1(n∈{N^*})$.
(2)${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(2n+1)(2n+3)}=\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$.
Tn=b1+b2+…+bn=$\frac{1}{2}[(\frac{1}{3}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{7})+…+(\frac{1}{2n+1}-\frac{1}{2n+3})]$=$\frac{n}{3(2n+3)}$.
∵λ≤Tn對一切n∈N*成立,∴λ≤T1.
∴$λ≤\frac{1}{15}$,即的最大值為$\frac{1}{15}$.
點評 本題考查了數列遞推關系、等差數列的通項公式、“裂項求和”方法與數列的單調性,考查了推理能力與計算能力,屬于中檔題.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,+∞) | B. | (-∞,-1) | C. | (-∞,+∞) | D. | [-1,1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{5}$ | B. | $\frac{5}{7}$ | C. | $±\frac{7}{12}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {-1,0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
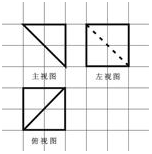
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com