
【題目】如圖,在平面四邊形![]() 中,
中,![]() 等邊三角形,
等邊三角形,![]() ,以
,以![]() 為折痕將
為折痕將![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
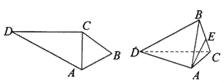
(1)設![]() 為
為![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見證明;(2) ![]()
【解析】
(1)推導出![]() 平面
平面![]() ,從而
,從而![]() ,再求出
,再求出![]() ,由此能證明
,由此能證明![]() 平面
平面![]() .
.
(2)由![]() 平面
平面![]() ,知
,知![]() 即為
即為![]() 與平面
與平面![]() 所成角,從而在直角
所成角,從而在直角![]() 中,
中,![]() ,以
,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() 所在的方向作為
所在的方向作為![]() 軸、
軸、![]() 軸的正方向,建立空間直角坐標系
軸的正方向,建立空間直角坐標系![]() .利用向量法能求出二面角
.利用向量法能求出二面角![]() 的余弦值.
的余弦值.
證明:(1)因為平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .
.
在等邊![]() 中,因為
中,因為![]() 為
為![]() 的中點,所以
的中點,所以![]() .
.
因為![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:由(1)知![]() 平面
平面![]() ,所以
,所以![]() 即為
即為![]() 與平面
與平面![]() 所成角,
所成角,
于是在直角![]() 中,
中,![]() .
.
以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() 所在的方向作為
所在的方向作為![]() 軸、
軸、![]() 軸的正方向,建立如圖所示的空間直角坐標系
軸的正方向,建立如圖所示的空間直角坐標系![]() .
.
設等邊![]() 的邊長為
的邊長為![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則 ,即
,即 ,
,
令![]() ,則
,則![]() ,
,![]() ,于是
,于是![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則 ,即
,即 ,
,
解得![]() ,令
,令![]() ,則
,則![]() ,于是
,于是![]() .
.
所以 .
.
由題意知二面角![]() 為銳角,所以二面角
為銳角,所以二面角![]() 的余弦值為
的余弦值為![]() .
.



科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,
中,![]() ,
,![]() .M為CD的中點.
.M為CD的中點.

(1)若點E為PC的中點,求證:BE∥平面PAD;
(2)當平面PBD⊥平面ABCD時,求點A到平面CEM的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改革開放以來,伴隨著我國經濟持續增長,戶均家庭教育投入![]() 戶均家庭教育投入是指一個家庭對家庭成員教育投入的總和
戶均家庭教育投入是指一個家庭對家庭成員教育投入的總和![]() 也在不斷提高
也在不斷提高![]() 我國某地區2012年至2018年戶均家庭教育投入
我國某地區2012年至2018年戶均家庭教育投入![]() 單位:千元
單位:千元![]() 的數據如表:
的數據如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
戶均家庭教育投入y |
|
|
|
|
|
|
|
![]() 求y關于t的線性回歸方程;
求y關于t的線性回歸方程;
![]() 利用
利用![]() 中的回歸方程,分析2012年至2018年該地區戶均家庭教育投入的變化情況,并預測2019年該地區戶均家庭教育投入是多少.
中的回歸方程,分析2012年至2018年該地區戶均家庭教育投入的變化情況,并預測2019年該地區戶均家庭教育投入是多少.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為: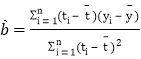 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量表得如下頻數分布表:
質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
頻數 | 6 | 26 | 38 | 22 | 8 |
(I)在答題卡上作出這些數據的頻率分布直方圖:

(II)估計這種產品質量指標值的平均數及方差(同一組中的數據用該組區間的中點值作代表);
(III)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于95的產品至少要占全部產品的80%”的規定?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把半橢圓![]() 與圓弧
與圓弧![]() 合成的曲線稱作“曲圓”,其中F為半橢圓的右焦點,A是圓弧
合成的曲線稱作“曲圓”,其中F為半橢圓的右焦點,A是圓弧![]() 與x軸的交點,過點F的直線交“曲圓”于P,Q兩點,則
與x軸的交點,過點F的直線交“曲圓”于P,Q兩點,則![]() 的周長取值范圍為______
的周長取值范圍為______
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年2月13日《煙臺市全民閱讀促進條例》全文發布,旨在保障全民閱讀權利,培養全民閱讀習慣,提高全民閱讀能力,推動文明城市和文化強市建設.某高校為了解條例發布以來全校學生的閱讀情況,隨機調查了200名學生每周閱讀時間![]() (單位:小時)并繪制如圖所示的頻率分布直方圖.
(單位:小時)并繪制如圖所示的頻率分布直方圖.

(1)求這200名學生每周閱讀時間的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組中的數據用該組區間的中間值代表);
(同一組中的數據用該組區間的中間值代表);
(2)由直方圖可以認為,目前該校學生每周的閱讀時間![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
(i)一般正態分布的概率都可以轉化為標準正態分布的概率進行計算:若![]() ,令
,令![]() ,則
,則![]() ,且
,且![]() .利用直方圖得到的正態分布,求
.利用直方圖得到的正態分布,求![]() .
.
(ii)從該高校的學生中隨機抽取20名,記![]() 表示這20名學生中每周閱讀時間超過10小時的人數,求
表示這20名學生中每周閱讀時間超過10小時的人數,求![]() (結果精確到0.0001)以及
(結果精確到0.0001)以及![]() 的數學期望.
的數學期望.
參考數據:![]() ,
,![]() .若
.若![]() ,則
,則![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點E(﹣4,0)和F(4,0),過點E的直線l與過點F的直線m相交于點M,設直線l的斜率為k1,直線m的斜率為k2,如果k1k2![]() .
.
(1)記點M形成的軌跡為曲線C,求曲線C的軌跡方程.
(2)已知P(2,m)、Q(2,﹣m)(m>0)是曲線C上的兩點,A,B是曲線C上位于直線PQ兩側的動點,當A,B運動時,滿足∠APQ=∠BPQ,試問直線AB的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() 在圓柱
在圓柱![]() 的底面圓
的底面圓![]() 上,
上,![]() 為圓
為圓![]() 的直徑.
的直徑.
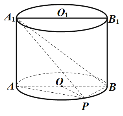
(1)若圓柱![]() 的體積
的體積![]() 為
為![]() ,
,![]() ,
,![]() ,求異面直線
,求異面直線![]() 與
與![]() 所成的角(用反三角函數值表示結果);
所成的角(用反三角函數值表示結果);
(2)若圓柱![]() 的軸截面是邊長為2的正方形,四面體
的軸截面是邊長為2的正方形,四面體![]() 的外接球為球
的外接球為球![]() ,求
,求![]() 兩點在球
兩點在球![]() 上的球面距離.
上的球面距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com