
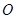 的直徑,AC是弦,
的直徑,AC是弦, ,垂足為D,AC平分
,垂足為D,AC平分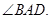
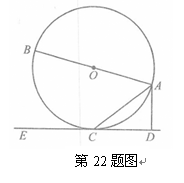
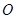 的切線;
的切線;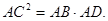
 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源:不詳 題型:解答題
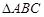 內接于⊙
內接于⊙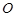 ,
, 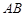 是⊙
是⊙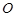 的直徑,
的直徑,  是過點
是過點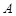 的直線, 且
的直線, 且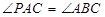 .
.
 是⊙
是⊙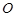 的切線;
的切線; 交
交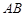 于點
于點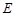 ,
,  ,
,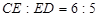 ,
,  , 求
, 求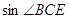 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
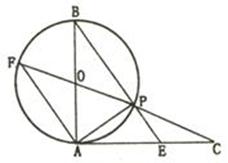

查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
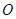 為極點,
為極點,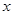 軸的正半軸為極軸,已知點
軸的正半軸為極軸,已知點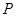 的直角坐標為
的直角坐標為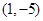 ,點
,點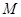 的極坐標為
的極坐標為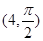 ,若直線
,若直線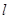 過點
過點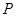 ,且傾斜角為
,且傾斜角為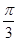 ,圓
,圓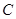 以
以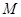 為 圓心、
為 圓心、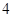 為半徑。
為半徑。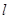 的參數方程和圓
的參數方程和圓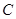 的極坐標方程;
的極坐標方程;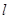 和圓
和圓 的位置關系。
的位置關系。查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
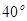 ,則∠DEB___________
,則∠DEB___________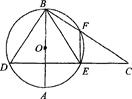
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com