考點:其他不等式的解法
專題:計算題,函數的性質及應用,不等式的解法及應用
分析:對a討論,a>1和0<a<1兩種情況,運用對數的換底公式,全部以a為底,運用對數函數的單調性,及換元法,令f(t)=loga(t+1)•loga(1+t2)-loga3•loga5,判斷單調性,再由二次不等式的解法與判別式的關系,即可得到所求范圍.
解答:
解:①當a>1時,log
(
+1)•log
5(x
2+ax+6)+log
a3≥0
即為-log
a(
+1)•log
5(x
2+ax+6)+log
a3≥0,
令
=t(t≥0),則-log
a(t+1)•log
5(1+t
2)+log
a3≥0,
由于log
a3>0,log
a5>0,
則有log
a(t+1)•log
a(1+t
2)-log
a3•log
a5≤0,
令f(t)=log
a(t+1)•log
a(1+t
2)-log
a3•log
a5,則f(t)遞增,
且f(2)=0,即有f(t)≤f(2),即有t≤2.
即有0≤x
2+ax+5≤4,由于只有一解,則判別式a
2-4=0,解得,a=2;
②當0<a<1時,log
(
+1)•log
5(x
2+ax+6)+log
a3≥0
即為-log
a(
+1)•log
5(x
2+ax+6)+log
a3≥0,
令
=t(t≥0),則-log
a(t+1)•log
5(1+t
2)+log
a3≥0,
由于log
a3<0,log
a5<0,
則有log
a(t+1)•log
a(1+t
2)-log
a3•log
a5≥0,
令f(t)=log
a(t+1)•log
a(1+t
2)-log
a3•log
a5,則f(t)遞減,
且f(2)=0,即有f(t)≥f(2),即有t≤2.
即有x
2+ax+5≤4,由于判別式a
2-4<0,則不等式的解集為∅.
綜上可得,a的取值范圍為{2}.
點評:本題考查對數不等式的解法,考查對數函數的單調性和運用,考查分類討論的思想方法,考查運算化簡能力,屬于中檔題和易錯題.



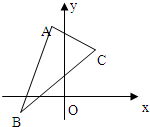 如圖,已知△ABC三個頂點是A(-1,4),B(-2,-1),C(2,3)
如圖,已知△ABC三個頂點是A(-1,4),B(-2,-1),C(2,3) 如圖,已知圓柱體底面圓的半徑為
如圖,已知圓柱體底面圓的半徑為