Question

14．在平面四邊形ABCD中，已知sin∠ADC=$\frac{4}{5}$，$\overrightarrow{AB}$•$\overrightarrow{AC}$=0，|$\overrightarrow{AB}$|=1，|$\overrightarrow{AC}$|=8，求|$\overrightarrow{BD}$|的最大值4$\sqrt{2}$+5 ．

Answer 1

分析 求出△ACD的外接圓半徑和圓心，根據點與圓的位置關系即可得出BD的最大值．

解答 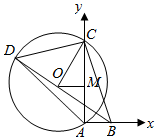解：設△ACD的外接圓半徑為r，則2r=$\frac{AC}{sin∠ADC}$=10，
∴r=5．
設△ACD的外接圓圓心為O，則O到AC的距離OM=$\sqrt{{r}^{2}-（\frac{AC}{2}）^{2}}$=3，
以AB，AC為坐標軸建立空間坐標系，則O（-3，4）或O（3，4），
∵D在圓O上，
∴當圓心為（-3，4），且B，O，D三點共線時，BD取得最大值．
∴|BD|的最大值為|OB|+r=$\sqrt{（-3-1）^{2}+{4}^{2}}$+5=4$\sqrt{2}$+5．
故答案為：4$\sqrt{2}$+5．

點評 本題考查了平面向量在幾何中的應用，屬于中檔題．