
分析 設生產A款手機x臺,B款手機y臺,利潤總和為z,得出約束條件表示的可行域,根據可行域得出目標函數取得最大值時的最優解.
解答  解:設生產A款手機x臺,B款手機y臺,利潤總和為z,
解:設生產A款手機x臺,B款手機y臺,利潤總和為z,
則$\left\{\begin{array}{l}{3x+y≤300}\\{x+3y≤300}\\{x+y≤120}\\{x≥0,y≥0}\end{array}\right.$,目標函數z=1000x+2000y,
做出可行域如圖所示:
將z=1000x+2000變形,得y=-$\frac{1}{2}$x+$\frac{z}{2000}$,
由圖象可知,當直線經過點M時,z取得最大值.
解方程組$\left\{\begin{array}{l}{x+3y=300}\\{x+y=120}\end{array}\right.$,得M的坐標為(30,90).
所以當x=30,y=90時,zmax=1000×30+2000×90=210000.
故生產產品A、產品B的利潤之和的最大值為210000元.
點評 本題考查了簡單的線性規劃的應用,做出約束條件,根據可行域判斷最優解的位置是關鍵,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $({\sqrt{6},\sqrt{7}}]$ | B. | $({0,\sqrt{7}}]$ | C. | $({\frac{{2\sqrt{42}}}{5},\sqrt{7}}]$ | D. | (6,7] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (x-2)2+(y+1)2=3 | B. | (x+2)2+(y-1)2=3 | C. | (x-2)2+(y+1)2=9 | D. | (x+2)2+(y-1)2=9 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
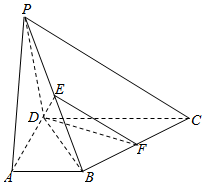 在四棱錐P-ABCD中,底面ABCD為直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分別是PB,BC的中點.
在四棱錐P-ABCD中,底面ABCD為直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分別是PB,BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com