
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
分析 設等腰直角三角形OAB的頂點A(x1,y1),B(x2,y2),利用OA=OB可求得x1=x2,進而可求得AB=4p,從而可得S△OAB.設過點N的直線方程為y=k(x+1),代入y2=4x,過M作準線的垂線,垂足為A,則|MF|=|MA|,考慮直線與拋物線相切及傾斜角為0°,即可得出p.設M 到準線的距離等于d,由拋物線的定義,化簡為 $\frac{|OM|}{|MF|}$=$\frac{|MO|}p9vv5xb5$=$\sqrt{\frac{{m}^{2}+4m}{(m+1)^{2}}}$,換元,利用基本不等式求得最大值.
解答 解:設等腰直角三角形OAB的頂點A(x1,y1),B(x2,y2),則y12=2px1,y22=2px2.
由OA=OB得:x12+y12=x22+y22,
∴x12-x22+2px1-2px2=0,即(x1-x2)(x1+x2+2p)=0,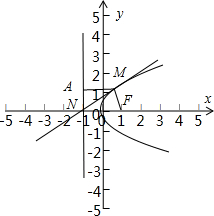
∵x1>0,x2>0,2p>0,
∴x1=x2,即A,B關于x軸對稱.
∴直線OA的方程為:y=xtan45°=x,
與拋物線聯立,解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2p}\\{y=2p}\end{array}\right.$,
故AB=4p,
∴S△OAB=$\frac{1}{2}$×2p×4p=4p2.
∵△AOB的面積為16,∴p=2;
焦點F(1,0),設M(m,n),則n2=4m,m>0,設M 到準線x=-1的距離等于d,
則$\frac{|OM|}{|MF|}$=$\frac{|MO|}p9vv5xb5$=$\sqrt{\frac{{m}^{2}+4m}{(m+1)^{2}}}$.
令 m+1=t,t>1,則$\frac{|OM|}{|MF|}$=$\sqrt{-3(\frac{1}{t}-\frac{1}{3})^{2}+\frac{4}{3}}$≤$\frac{2\sqrt{3}}{3}$(當且僅當 t=3時,等號成立).
故 $\frac{|OM|}{|MF|}$的最大值為$\frac{2\sqrt{3}}{3}$,
故選C.
點評 本題考查拋物線的簡單性質,求得A,B關于x軸對稱是關鍵,考查拋物線的定義,基本不等式的應用,體現了換元的思想,正確運用拋物線的定義是關鍵,屬于難題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | ∅ | B. | {(1,1)} | C. | {(x,y)|x+y-2=0} | D. | {(x,y)|3x-2y-1=0} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
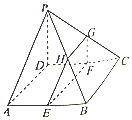 如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,底面ABCD為菱形,.點分E,F,G,H別是棱AB,CD,PC,PB上共面的四點,且BC∥EF.
如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,底面ABCD為菱形,.點分E,F,G,H別是棱AB,CD,PC,PB上共面的四點,且BC∥EF. 查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
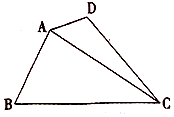 如圖,四邊形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,則線段AC長度的取值范圍是( )
如圖,四邊形ABCD中,∠BAD=135°,∠ADC=120°,∠BCD=45°,∠ABC=60°,BC=$\sqrt{3}$,則線段AC長度的取值范圍是( )| A. | $[{\sqrt{2},\sqrt{3}})$ | B. | $[{\frac{3}{2},\sqrt{3}})$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({\frac{3}{2},\sqrt{3}})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com