
���}Ŀ����֪�E�A![]() ��һ��(g��)���c(di��n)�c���タ
��һ��(g��)���c(di��n)�c���タ![]() �Ľ��c(di��n)�غϣ��Ҵ˒��タ�Ĝ�(zh��n)�����E�A
�Ľ��c(di��n)�غϣ��Ҵ˒��タ�Ĝ�(zh��n)�����E�A![]() �صõ����L(zh��ng)��
�صõ����L(zh��ng)��![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2��ֱ��![]() ���E�A
���E�A![]() ��
��![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() �����c(di��n)��
�����c(di��n)��![]() ��ֱ��
��ֱ��![]() �Ǿ���
�Ǿ���![]() �Ĵ�ֱƽ�־���ԇ��(w��n)ֱ��
�Ĵ�ֱƽ�־���ԇ��(w��n)ֱ��![]() �Ƿ��^(gu��)���c(di��n)�����ǣ�Ո(q��ng)���ԓ���c(di��n)������(bi��o)�������ǣ�Ո(q��ng)�f(shu��)�����ɣ�
�Ƿ��^(gu��)���c(di��n)�����ǣ�Ո(q��ng)���ԓ���c(di��n)������(bi��o)�������ǣ�Ո(q��ng)�f(shu��)�����ɣ�
���𰸡���1��![]() ����2��ֱ��
����2��ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() ��ԔҊ(ji��n)����.
��ԔҊ(ji��n)����.
��������
��1�����}��ó�![]() �����}��֪�c(di��n)
�����}��֪�c(di��n)![]() �ڙE�A
�ڙE�A![]() �ϣ��ɴ˵ó��P(gu��n)��
�ϣ��ɴ˵ó��P(gu��n)��![]() ��
��![]() �ķ��̽M�����
�ķ��̽M�����![]() ��
��![]() ��ֵ�����ɵó��E�A
��ֵ�����ɵó��E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���ⷨһ�����}���֪��ֱ��![]() ��б�ʲ����㣬Ȼ���ֱ��
��б�ʲ����㣬Ȼ���ֱ��![]() ��б�ʴ����Ҳ������ֱ��
��б�ʴ����Ҳ������ֱ��![]() ��б�ʲ����ڃɷN��rӑՓ���ڵ�һ�N��r�£��O(sh��)ֱ��
��б�ʲ����ڃɷN��rӑՓ���ڵ�һ�N��r�£��O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() ��
��![]() ����ֱ��
����ֱ��![]() �ķ����c�E�A
�ķ����c�E�A![]() �ķ���(li��n)�����г��f�_(d��)��������
�ķ���(li��n)�����г��f�_(d��)��������![]() �ó�
�ó�![]() ������(xi��)��ֱ��
������(xi��)��ֱ��![]() �ķ��̣��ɴ˿ɵó�ֱ��
�ķ��̣��ɴ˿ɵó�ֱ��![]() ���^(gu��)���c(di��n)������(bi��o)���ڵڶ��N��r�¿ɵó�ֱ��
���^(gu��)���c(di��n)������(bi��o)���ڵڶ��N��r�¿ɵó�ֱ��![]() ��
��![]() �S�����ɵó�ֱ��
�S�����ɵó�ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() ���ɴ˵ó��Y(ji��)Փ��
���ɴ˵ó��Y(ji��)Փ��
�ⷨ�������}���֪��ֱ��![]() ��б�ʲ����㣬Ȼ���ֱ��
��б�ʲ����㣬Ȼ���ֱ��![]() ��б�ʴ����Ҳ������ֱ��
��б�ʴ����Ҳ������ֱ��![]() ��б�ʲ����ڃɷN��rӑՓ���ڵ�һ�N��r�£����c(di��n)��ɵó�ֱ��
��б�ʲ����ڃɷN��rӑՓ���ڵ�һ�N��r�£����c(di��n)��ɵó�ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ���Ɍ�(xi��)��ֱ��
���Ɍ�(xi��)��ֱ��![]() �ķ��̣����ɵó�ֱ��
�ķ��̣����ɵó�ֱ��![]() ���^(gu��)���c(di��n)������(bi��o)���ڵڶ��N��r�¿ɵó�ֱ��
���^(gu��)���c(di��n)������(bi��o)���ڵڶ��N��r�¿ɵó�ֱ��![]() ��
��![]() �S�����ɵó�ֱ��
�S�����ɵó�ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() ���ɴ˵ó��Y(ji��)Փ.
���ɴ˵ó��Y(ji��)Փ.
��1�����タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ����(zh��n)����
����(zh��n)����![]() .
.
���ڒ��タ![]() �Ĝ�(zh��n)��
�Ĝ�(zh��n)��![]() �ؙE�A
�ؙE�A![]() �������L(zh��ng)��
�������L(zh��ng)��![]() ��
��
�t�c(di��n)![]() �ڙE�A
�ڙE�A![]() �ϣ��t��
�ϣ��t��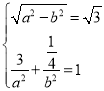 �����
�����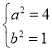 ��
��
��ˣ��E�A![]() �Ę�(bi��o)��(zh��n)���̞�
�Ę�(bi��o)��(zh��n)���̞�![]() ��
��
��2����һ���@Ȼ�c(di��n)![]() �ڙE�A
�ڙE�A![]() ��(n��i)������
��(n��i)������![]() ����ֱ��
����ֱ��![]() ��б�ʲ���
��б�ʲ���![]() .
.
��(d��ng)ֱ��![]() ��б�ʴ����Ҳ���
��б�ʴ����Ҳ���![]() �r(sh��)����֪
�r(sh��)����֪![]() ���O(sh��)ֱ��
���O(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
����E�A���̲�����(ji��n)�ã�![]() .
.
�O(sh��)![]() ��
��![]() ���t
���t![]() �����
�����![]() .
.
��?y��n)�ֱ��![]() �Ǿ���
�Ǿ���![]() �Ĵ�ֱƽ�־���
�Ĵ�ֱƽ�־���
��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ����
����![]() .
.
��![]() ���˕r(sh��)
���˕r(sh��)![]() ��
��![]() ������ֱ��
������ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() ��
��
��(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)����֪
��б�ʲ����ڕr(sh��)����֪![]() ���˕r(sh��)ֱ��
���˕r(sh��)ֱ��![]() ����ֱ��
����ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() .
.
�C��������ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() ��
��
�������@Ȼ�c(di��n)![]() �ڙE�A
�ڙE�A![]() ��(n��i)������
��(n��i)������![]() ����ֱ��
����ֱ��![]() ��б�ʲ���
��б�ʲ���![]() .
.
��(d��ng)ֱ��![]() ��б�ʴ����Ҳ���
��б�ʴ����Ҳ���![]() �r(sh��)���O(sh��)
�r(sh��)���O(sh��)![]() ��
��![]() ��
��
�t��![]() ��
��![]() ��
��
��ʽ���p��![]() ��
��
�ɾ���![]() �����c(di��n)��
�����c(di��n)��![]() ���t
���t![]() ��
��![]() ��
��
��ֱ��![]() ��б��
���![]() ��
��
��?y��n)�ֱ��![]() �Ǿ���
�Ǿ���![]() �Ĵ�ֱƽ�־���
�Ĵ�ֱƽ�־���
��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ����
����![]() .
.
��![]() ���˕r(sh��)
���˕r(sh��)![]() ��
��![]() ������ֱ��
������ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() ��
��
��(d��ng)ֱ��![]() ��б�ʲ����ڕr(sh��)����֪
��б�ʲ����ڕr(sh��)����֪![]() ���˕r(sh��)ֱ��
���˕r(sh��)ֱ��![]() ����ֱ��
����ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]()
�C��������ֱ��![]() �^(gu��)���c(di��n)
�^(gu��)���c(di��n)![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У���(d��ng)�c(di��n)
����(d��ng)�c(di��n)![]() ������
������![]() �����c(di��n)
�����c(di��n)![]() �ľ��x��
�ľ��x��![]() ���c�c(di��n)
���c�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ��֮��ӛ��
��֮��ӛ��![]() ����
����![]() .
.
�������c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
�����O(sh��)�^(gu��)�c(di��n)![]() ��ֱ��
��ֱ��![]() �c܉�E
�c܉�E![]() ����
����![]() ���c(di��n)����
���c(di��n)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
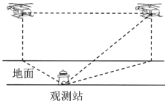
���}Ŀ��2019��10��1�գ��ڑcף���Ї�(gu��)����70����醱��У����҇�(gu��)�������Ƶ�܊���w�C(j��)��܊�ßo(w��)�˙C(j��)�ȅ�醺����b����벻���wԽ�찲�T(m��n)����܊���������ģ������˲�Ŀ���w�ІT�߳����w�м��g(sh��)�x���_(k��i)�D���Ӗ(x��n)���ͿƌW(xu��)�Ĕ�(sh��)��(j��)������һ���w��Ӗ(x��n)���У������^�y(c��)վ�^�y(c��)��һ�܅��ֱ���w�C(j��)��![]() ǧ��/С�r(sh��)���ٶ���ͬһ�߶������|�w�У���D����һ���^�y(c��)��ԓ�w�C(j��)�ڱ�ƫ��
ǧ��/С�r(sh��)���ٶ���ͬһ�߶������|�w�У���D����һ���^�y(c��)��ԓ�w�C(j��)�ڱ�ƫ��![]() �ķ����ϣ�1��犺�ڶ����^�y(c��)��ԓ�w�C(j��)�ڱ�ƫ�|
�ķ����ϣ�1��犺�ڶ����^�y(c��)��ԓ�w�C(j��)�ڱ�ƫ�|![]() �ķ����ϣ����Ǟ�
�ķ����ϣ����Ǟ�![]() ���tֱ���C(j��)�w�еĸ߶Ȟ�________ǧ�ף����Y(ji��)��������̖(h��o)��
���tֱ���C(j��)�w�еĸ߶Ȟ�________ǧ�ף����Y(ji��)��������̖(h��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��������![]() ��ÿ��(g��)�c(di��n)�ęM����(bi��o)���L(zh��ng)��ԭ��(l��i)��
��ÿ��(g��)�c(di��n)�ęM����(bi��o)���L(zh��ng)��ԭ��(l��i)��![]() ��(�v����(bi��o)��׃),�õ�
��(�v����(bi��o)��׃),�õ�![]() �ĈD��,�t�����f(shu��)�����_���ǣ� ��
�ĈD��,�t�����f(shu��)�����_���ǣ� ��
A.![]() �ĈD���P(gu��n)��ֱ��
�ĈD���P(gu��n)��ֱ��![]() ��(du��)�Q(ch��ng)
��(du��)�Q(ch��ng)
B.![]() ��
��![]() �ϵ�ֵ��?y��n)?/span>
�ϵ�ֵ��?y��n)?/span>![]()
C.![]() �ĈD���P(gu��n)���c(di��n)
�ĈD���P(gu��n)���c(di��n)![]() ��(du��)�Q(ch��ng)
��(du��)�Q(ch��ng)
D.![]() �ĈD�����
�ĈD�����![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ��(g��)��λ�L(zh��ng)�ȵõ�
��(g��)��λ�L(zh��ng)�ȵõ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �ķ��̞�
�ķ��̞�![]() ���E�A
���E�A![]() ���x�����������p����
���x�����������p����![]() ���x���ʵĵ���(sh��)���E�A
���x���ʵĵ���(sh��)���E�A![]() �Ķ��S�L(zh��ng)���ڒ��タ
�Ķ��S�L(zh��ng)���ڒ��タ![]() ��һ�c(di��n)
��һ�c(di��n)![]() �����タ���c(di��n)
�����タ���c(di��n)![]() �ľ��x.
�ľ��x.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����ֱ��![]() �c�E�A
�c�E�A![]() �ăɂ�(g��)���c(di��n)��
�ăɂ�(g��)���c(di��n)��![]() ��
��![]() ���c(di��n)����֪�A
���c(di��n)����֪�A![]() ��
��![]() �c
�c![]() �S�Ľ��c(di��n)�քe��
�S�Ľ��c(di��n)�քe��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() �S�������S������ֱ��
�S�������S������ֱ��![]() �c�A
�c�A![]() ������
������![]() ����e�c
����e�c![]() ����e�˷e�����ֵ.
����e�˷e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�ƽ��
�У�ƽ��![]() ����
����![]() �������
�����е���![]() ��������Σ�
���������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n).
�����c(di��n).
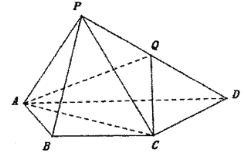
��1���C����![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
(1)��(sh��)![]() ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g��
(2)![]() ��(n��i)��
��(n��i)��![]() �Č�(du��)߅�քe��
�Č�(du��)߅�քe��![]() ����
����![]() ��
��![]() ��
��![]() ����
����![]() ��ԇ���
��ԇ���![]() �ͽ�
�ͽ�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() ��
��![]() .
.
��1����(d��ng)![]() �r(sh��)����ʽ
�r(sh��)����ʽ![]() �Ľ⼯��
�Ľ⼯��
��2����֪![]() ���������
���������![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ������
������![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��)��
����Ȼ��(du��)��(sh��)�ĵה�(sh��)��![]() .
.
��1�����C��![]() ��
��
��2����(du��)������![]() ��
��![]() ���������
���������![]() ��ȡֵ������
��ȡֵ������
��3��������![]() ��ʹ
��ʹ![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com