
���� ����������タ�Ĝ�(zh��n)�����̣�����ֱ���c�A��λ���P(gu��n)ϵ�г����̣����P�������タ���ķ��̣�
�����O(sh��)N��t��$\frac{{t}^{2}}{2}$�����A��O��ֱ��PQ�ľ��x��$\frac{\frac{{t}^{2}}{2}}{\sqrt{1+{t}^{2}}}$������c(di��n)F��ֱ��PQ�ľ��x����ʾ����FPQ��e�������䷽���������FPQ��e�����ֵ��
��� �⣺������?y��n)钁�タ���Ĝ�(zh��n)�����̞飺y=-$\frac{p}{2}$��
��ֱ�����AO��x2+y2=4���صõ����L(zh��ng)��$\sqrt{15}$��
����$\sqrt{4-��\frac{p}{2}��^{2}}$=$\frac{1}{2}$$\sqrt{15}$���p=1��
��˒��タ���ķ��̞�x2=2y����4�֣���
�����O(sh��)N��t��$\frac{{t}^{2}}{2}$������y��=xֱ֪��PQ�ķ��̞飺y-$\frac{{t}^{2}}{2}$=t��x-t������y=tx-$\frac{{t}^{2}}{2}$����6�֣�
��?y��n)�A��O��ֱ��PQ�ľ��x��$\frac{\frac{{t}^{2}}{2}}{\sqrt{1+{t}^{2}}}$������|PQ|=2$\sqrt{4-\frac{{t}^{4}}{4��1+{t}^{2}��}}$����7�֣�
�O(sh��)�c(di��n)F��ֱ��PQ�ľ��x��d���td=$\frac{\frac{1}{2}+\frac{{t}^{2}}{2}}{\sqrt{1+{t}^{2}}}$=$\frac{1}{2}\sqrt{1+{t}^{2}}$���� 8�֣�
���ԣ���FPQ����eS=$\frac{1}{2}$|PQ|d=$\frac{1}{4}$$\sqrt{-{t}^{4}+16{t}^{2}+16}$=$\frac{1}{4}$$\sqrt{-��{t}^{2}-8��^{2}+80}$��$\sqrt{80}$=$\sqrt{5}$��11�֣�
��(d��ng)t=��2$\sqrt{2}$�r(sh��)ȡ����=������(j��ng)�z�(y��n)�˕r(sh��)ֱ��PQ�c�AO�ཻ���M���}�⣮
�C�Ͽ�֪����FPQ����e�����ֵ��$\sqrt{5}$����12�֣���
�c(di��n)�u(p��ng) ���}����ֱ���c�A��λ���P(gu��n)ϵ�����钁�タ���̣�������������e��Ӌ(j��)�㣬����W(xu��)��������Q���}�������������Йn�}��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
| A�� | 1 | B�� | 0 | C�� | -1 | D�� | ���_�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
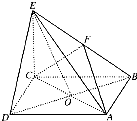 �����FE-ABCD�У�����ABCD�������Σ�AC�cBD�����c(di��n)O��EC�͵���ABCD��F(xi��n)��BE���c(di��n)��CE=2��AB=2��
�����FE-ABCD�У�����ABCD�������Σ�AC�cBD�����c(di��n)O��EC�͵���ABCD��F(xi��n)��BE���c(di��n)��CE=2��AB=2���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ��x���}
| A�� | 3-i | B�� | 1+3i | C�� | 3+i | D�� | 1-3i |
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com