
甲廠以x千克/小時的速度勻速生產某種產品(生產條件要求1≤x≤10),每一小時可獲得的利潤是100(5x+1﹣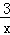 )元.
)元.
(1)求證:生產a千克該產品所獲得的利潤為100a(5+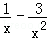 )元;
)元;
(2)要使生產900千克該產品獲得的利潤最大,問:甲廠應該選取何種生產速度?并求此最大利潤.
(1)見解析(2)甲廠應以6千克/小時的速度生產,可獲得最大利潤457500元
【解析】
試題分析:1)生產a千克該產品所用的時間是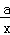 小時,
小時,
∵每一小時可獲得的利潤是100(5x+1﹣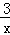 )元,∴獲得的利潤為100(5x+1﹣
)元,∴獲得的利潤為100(5x+1﹣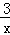 )×
)×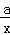 元.
元.
因此生產a千克該產品所獲得的利潤為100a(5+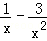 )元.
)元.
(2)生產900千克該產品獲得的利潤為90000(5+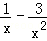 ),1≤x≤10.
),1≤x≤10.
設f(x)=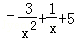 ,1≤x≤10.
,1≤x≤10.
則f(x)=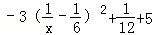 ,當且僅當x=6取得最大值.
,當且僅當x=6取得最大值.
故獲得最大利潤為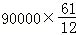 =457500元.
=457500元.
考點:函數模型的選擇與應用;二次函數在閉區間上的最值
點評:正確理解題意和熟練掌握二次函數的單調性是解題的關鍵


 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:高中數學 來源: 題型:
| 3 |
| x |
| 1 |
| x |
| 3 |
| x2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 | x |
查看答案和解析>>
科目:高中數學 來源: 題型:
甲廠以x千克/小時的速度勻速生產某種產品(生產條件要求1≤x≤10),每小時可獲得的利潤是100![]() 元.
元.
(1)求證:生產a千克該產品所獲得的利潤為100a![]() 元;
元;
(2)要使生產900千克該產品獲得的利潤最大,問:甲廠應該選取何種生產速度?并求此最大利潤.
查看答案和解析>>
科目:高中數學 來源:2013年全國普通高等學校招生統一考試理科數學(上海卷解析版) 題型:解答題
甲廠以x 千克/小時的速度運輸生產某種產品(生產條件要求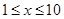 ),每小時可獲得利潤是
),每小時可獲得利潤是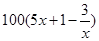 元.
元.
(1)要使生產該產品2小時獲得的利潤不低于3000元,求x的取值范圍;
(2)要使生產900千克該產品獲得的利潤最大,問:甲廠應該選取何種生產速度?并求最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com