
分析 (1)由已知中f(x)=x3-ax+b(a,b∈R),我們易求出函數的導函數f′(x),進而給出函數g(x)=lnx-$\frac{a}{6}$[f′(x)+a]-2x的解析式,若函數g(x)存調遞減區間,則g′(x)=$\frac{1}{x}$-ax-2<0在(0,+∞)上有解,構造函數h(x)=$\frac{1-2x}{{x}^{2}}$,求出其最小值,即可得到答案.
(2)由(1)中導函數f′(x)的解析式,我們設出切點坐標,則可以得到直線的切線方程,由于切線過A點,將A點坐標代入即可得到關于參數的方程,又由已知中過點A(1,0)的曲線C的切線恰有三條,則對應方程恰有三個不同的根,構造函數后,可以轉化為函數恰有三個零點,結合三次函數的圖象性質,判斷出函數的極小值小于0,極大值大于0,構造關于參數的方程組,解方程組,即可得到答案.
解答 解:(1)∵f′(x)=3x2-a,
∴g(x)=lnx-$\frac{a}{6}$[f′(x)+a]-2x=lnx-$\frac{a}{2}$x2-2x(x>0)
∴g′(x)=$\frac{1}{x}$-ax-2
若使g(x) 存在單調減區間,
則g′(x)=$\frac{1}{x}$-ax-2<0在(0,+∞)上有解,
即a>$\frac{1-2x}{{x}^{2}}$在(0,+∞)上有解,
設h(x)=$\frac{1-2x}{{x}^{2}}$=($\frac{1}{x}$-1)2-1,
則h(x)的最小值為-1,
若a>$\frac{1-2x}{{x}^{2}}$在(0,+∞)上有解,
則a>-1;
(2)∵f′(x)=3x2-a,
過點A(1,0)作曲線C的切線,設切點坐標為(c,f(c))
則切線方程為 y-(c3-ac+b)=(3c2-a)(x-a)
即y=(3c2-a)x-2c3+b
又∵切線過A(1,0)點
則(3c2-a)-2c3+b=0
即-2c3+3c2-a+b=0
又由過點A(1,0)的曲線C的切線恰有三條,
∴方程-2c3+3c2-a+b=0恰好有三個根,
令h(c)=-2c3+3c2-a+b
則h′(c)=-6c2+6c
則函數h(c)=-2c3+3c2-a+b在c=0時取極小值,在c=1時取極大值,
若方程-2c3+3c2-a+b=0恰好有三個根,
則h(0)=-a+b<0,h(1)=1-a+b>0
即a,b滿足的關系式為0<a-b<1.
點評 本題考查的知識點是利用民數研究曲線上某點的切線方程,利用導數研究函數的單調性,其中根據函數的解析式,求出導函數的解析式是解答本題的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | 1+i | B. | 1-i | C. | $\frac{{\sqrt{2}}}{2}-\frac{{\sqrt{2}}}{2}i$ | D. | $\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{2}i$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
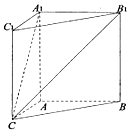 如圖,在三棱柱ABC-A1B1C1中,四邊形AA1C1C是邊長為4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如圖,在三棱柱ABC-A1B1C1中,四邊形AA1C1C是邊長為4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
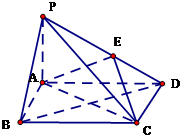 如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點.
如圖,四棱錐P-ABCD中,底面ABCD為矩形,PA⊥平面ABCD,E為PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{6}}}{4}$ | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com