
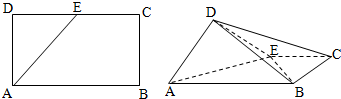
 如圖,ABCD是塊矩形硬紙板,其中AB=2AD=2
如圖,ABCD是塊矩形硬紙板,其中AB=2AD=2 ,E為DC中點,將它沿AE折成直二面角D-AE-B.
,E為DC中點,將它沿AE折成直二面角D-AE-B.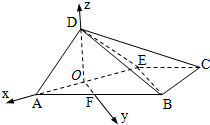 (Ⅰ)證明:由題設可知AD⊥DE,取AE中點O,
(Ⅰ)證明:由題設可知AD⊥DE,取AE中點O, ,∴OD⊥AE,
,∴OD⊥AE, ,
,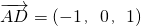 ,
,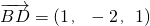 ,
, 是平面ABD的一個法向量,
是平面ABD的一個法向量,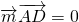 ,
,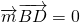 ,
,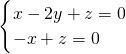 ,取x=1,則y=1,z=1,
,取x=1,則y=1,z=1, ,平面ADE的法向量
,平面ADE的法向量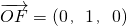 ,
,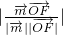 =
=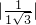 =
= .…(13分)
.…(13分) ,知OD⊥AE,由二面角D-AE-B為直二面角,知OD⊥平面ABCE由此能夠證明AD⊥平面BDE.
,知OD⊥AE,由二面角D-AE-B為直二面角,知OD⊥平面ABCE由此能夠證明AD⊥平面BDE.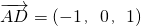 ,
,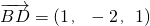 ,設
,設 是平面ABD的一個法向量,由
是平面ABD的一個法向量,由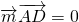 ,
,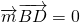 ,得
,得 ,平面ADE的法向量
,平面ADE的法向量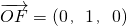 ,由向量法能求出二面角B-AD-E的平面角.
,由向量法能求出二面角B-AD-E的平面角.

 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:單選題
 ,則a1的取值范圍是
,則a1的取值范圍是查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com