
分析 (1)由P0=1,根據題設條件能求出P1、P2、P3.
(2)棋子跳到第n站,必是從第n-1站或第n-2站跳來的(2≤n≤100),從而${P_n}=\frac{1}{2}{P_{n-1}}+\frac{1}{2}{P_{n-2}}$,由此能證明{an}是公比為$-\frac{1}{2}$,首項為$-\frac{1}{2}$的等比數列(1≤n≤100).
(3)由a1+a2+…+a99=(P1-P0)+(P2-P1)+…+(P99-P98),能求出玩該游戲獲勝的概率.
解答 解:(1)∵P0=1,
∴${P_1}=\frac{1}{2}$,
${P_2}=\frac{1}{2}×\frac{1}{2}+\frac{1}{2}=\frac{3}{4}$,
${P_3}=\frac{1}{2}×\frac{1}{2}+\frac{3}{4}×\frac{1}{2}=\frac{5}{8}$.(3分)
證明:(2)棋子跳到第n站,必是從第n-1站或第n-2站跳來的(2≤n≤100),
所以${P_n}=\frac{1}{2}{P_{n-1}}+\frac{1}{2}{P_{n-2}}$,
∴${P_n}-{P_{n-1}}=-{P_{n-1}}+\frac{1}{2}{P_{n-1}}+\frac{1}{2}{P_{n-2}}=-\frac{1}{2}({P_{n-1}}-{P_{n-2}})$,
∴${a_n}=-\frac{1}{2}{a_{n-1}}(2≤n≤100)$,且${a_1}={P_1}-{P_0}=-\frac{1}{2}$,
故{an}是公比為$-\frac{1}{2}$,首項為$-\frac{1}{2}$的等比數列(1≤n≤100).(7分)
解:(3)由(2)知,a1+a2+…+a99=(P1-P0)+(P2-P1)+…+(P99-P98)
=$(-\frac{1}{2})+{(-\frac{1}{2})^2}+…+{(-\frac{1}{2})^{99}}$$⇒{P_{99}}-{P_0}=-\frac{{1-{{(-\frac{1}{2})}^{99}}}}{3}$$⇒{P_{99}}=\frac{2}{3}(1-\frac{1}{{{2^{100}}}})$.
故玩該游戲獲勝的概率為${P_{99}}=\frac{2}{3}(1-\frac{1}{{{2^{100}}}})$.(12分)
點評 本題考查概率的求法,考查等比數列的證明,是中檔題,解題時要認真審題,注意等比數列的性質的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
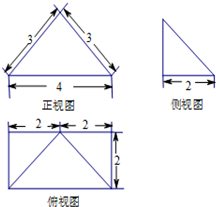 給出下列結論:
給出下列結論:查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | sinA<sinC | B. | tanA<tanC | C. | cosA<cosC | D. | $\frac{1}{tanA}$<$\frac{1}{tanC}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 有最大值$\frac{1}{2}$ | B. | 有最小值$\frac{1}{2}$ | C. | 有最大值$\frac{1}{4}$ | D. | 有最小值$\frac{1}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,1) | C. | (-∞,-1)∪(-1,1] | D. | (-∞,-1)∪(-1,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (12,30] | B. | (-∞,18] | C. | [18,+∞) | D. | (-12,18] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com