
已知函數 ,
, ,且
,且 在點
在點
 處的切線方程為
處的切線方程為 .
.
(1)求 的值;
的值;
(2)若函數 在區間
在區間 內有且僅有一個極值點,求
內有且僅有一個極值點,求 的取值范圍;
的取值范圍;
(3)設 為兩曲線
為兩曲線 ,
, 的交點,且兩曲線在交點
的交點,且兩曲線在交點 處的切線分別為
處的切線分別為 .若取
.若取 ,試判斷當直線
,試判斷當直線 與
與 軸圍成等腰三角形時
軸圍成等腰三角形時 值的個數并說明理由.
值的個數并說明理由.
(1) ;(2)
;(2) ;(3)2個
;(3)2個
【解析】
試題分析:(1)由函數 ,在點
,在點 處的切線方程為
處的切線方程為 .所以對函數求導,根據斜率為1以及過點(1,0)兩個條件即可求出結論.
.所以對函數求導,根據斜率為1以及過點(1,0)兩個條件即可求出結論.
(2)由函數 ,對函數
,對函數 求導,并令
求導,并令 可解得兩個根,由于函數
可解得兩個根,由于函數 在區間
在區間 內有且僅有一個極值點,
內有且僅有一個極值點, 的根在
的根在 內有且僅有一個根.所以通過分類討論即可求
內有且僅有一個根.所以通過分類討論即可求 的取值范圍.
的取值范圍.
(3)兩曲線在交點 處的切線分別為
處的切線分別為 .若取
.若取 ,當直線
,當直線 與
與 軸圍成等腰三角形時.通過求導求出兩函數的切線的斜率,即可得到這兩斜率不可能是相等,所以依題意可得到兩切線傾斜角有兩倍的關系,再通過解方程和函數的單調性的判斷即可得到結論.
軸圍成等腰三角形時.通過求導求出兩函數的切線的斜率,即可得到這兩斜率不可能是相等,所以依題意可得到兩切線傾斜角有兩倍的關系,再通過解方程和函數的單調性的判斷即可得到結論.
(1) ,∴
,∴ ,又
,又 ,
,
∴ . 3分
. 3分
(2) ;
;
∴
由 得
得 ,
,
∴ 或
或 . 5分
. 5分
∵ ,當且僅當
,當且僅當 或
或 時,函數
時,函數 在區間
在區間 內有且僅有一個極值點. 6分
內有且僅有一個極值點. 6分
若 ,即
,即 ,當
,當 時
時 ;當
;當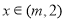 時
時 ,函數
,函數 有極大值點
有極大值點 ,
,
若 ,即
,即 時,當
時,當 時
時 ;當
;當 時
時 ,函數
,函數 有極大值點
有極大值點 ,
,
綜上, 的取值范圍是
的取值范圍是 . 8分
. 8分
(3)當 時,設兩切線
時,設兩切線 的傾斜角分別為
的傾斜角分別為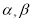 ,
,
則 ,
,
∵ , ∴
, ∴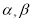 均為銳角, 9分
均為銳角, 9分
當 ,即
,即 時,若直線
時,若直線 能與
能與 軸圍成等腰三角形,則
軸圍成等腰三角形,則 ;當
;當 ,即
,即 時,若直線
時,若直線 能與
能與 軸圍成等腰三角形,則
軸圍成等腰三角形,則 .
.
由 得,
得, ,
,
得 ,即
,即 ,
,
此方程有唯一解 ,直線
,直線 能與
能與 軸圍成一個等腰三角形. 11分
軸圍成一個等腰三角形. 11分
由 得,
得,  ,
,
得 ,即
,即 ,
,
設 ,
, ,
,
當 時,
時, ,∴
,∴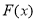 在
在 單調遞增,則
單調遞增,則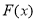 在
在 單調遞
單調遞
增,由于 ,且
,且 ,所以
,所以 ,則
,則 ,
,
即方程 在
在 有唯一解,直線
有唯一解,直線 能與
能與 軸圍成一個等腰三角形.
軸圍成一個等腰三角形.
因此,當 時,有兩處符合題意,所以直線
時,有兩處符合題意,所以直線 能與
能與 軸圍成等腰三角形時,
軸圍成等腰三角形時, 值的個數
值的個數
有2個. 14分
考點:1.導數的幾何意義.2.函數的極值.3.函數導數的應用.4.分析問題解決問題的能力.5.等價變換的數學思想.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源:2013-2014學年福建省廈門市高三5月適應性考試理科數學試卷(解析版) 題型:選擇題
已知圓 和圓
和圓 ,動圓M與圓
,動圓M與圓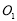 ,圓
,圓 都相切,動圓的圓心M的軌跡為兩個橢圓,這兩個橢圓的離心率分別為
都相切,動圓的圓心M的軌跡為兩個橢圓,這兩個橢圓的離心率分別為 ,
, (
(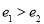 ),則
),則 的最小值是( )
的最小值是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省廈門市高三5月適應性考試文科數學試卷(解析版) 題型:選擇題
設向量 與
與 滿足
滿足 ,
, 在
在 方向上的投影為
方向上的投影為 ,若存在實數
,若存在實數 ,使得
,使得 與
與 垂直,則
垂直,則 =( )
=( )
A. B.1 C. 2 D. 3
B.1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省廈門市高三5月適應性考試文科數學試卷(解析版) 題型:選擇題
某市有大型超市200家、中型超市400家、小型超市1400家,為掌握各類超市的營業情況,現按分層抽樣方法抽取一個容量為100的樣本,應抽取中型超市( )
A. 70家 B.50家 C.20家 D.10家
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省三明市高三5月質量檢查理科數學試卷(解析版) 題型:填空題
對于集合 ,如果定義了一種運算“
,如果定義了一種運算“ ”,使得集合
”,使得集合 中的元素間滿足下列4個條件:
中的元素間滿足下列4個條件:
(ⅰ) ,都有
,都有 ;
;
(ⅱ) ,使得對
,使得對 ,都有
,都有 ;
;
(ⅲ) ,
,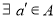 ,使得
,使得 ;
;
(ⅳ) ,都有
,都有 ,
,
則稱集合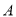 對于運算“
對于運算“ ”構成“對稱集”.
”構成“對稱集”.
下面給出三個集合及相應的運算“ ”:
”:
① ,運算“
,運算“ ”為普通加法;
”為普通加法;
② ,運算“
,運算“ ”為普通減法;
”為普通減法;
③ ,運算“
,運算“ ”為普通乘法.
”為普通乘法.
其中可以構成“對稱集”的有 .(把所有正確的序號都填上)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年福建省三明市高三5月質量檢查理科數學試卷(解析版) 題型:選擇題
如圖是某個四面體的三視圖,若在該四面體的外接球內任取一點,則點落在四面體內的概率為( )
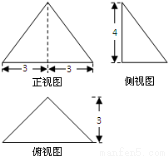
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年甘肅省武威市高三數學專題訓練選擇填空限時練六(解析版) 題型:選擇題
采用系統抽樣方法從480人中抽取16人做問卷調查,為此將他們隨機編號為1,2,…,480,分組后在第一組采用簡單隨機抽樣的方法抽到的號碼為8.抽到的16人中,編號落入區間[1,160]的人做問卷A,編號落入區間[161,320]的人做問卷B,其余的人做問卷C,則被抽到的人中,做問卷B的人數為( )
A.4 B.5 C.6 D.7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com