
 某工藝品廠要設計一個如圖Ⅰ所示的工藝品,現有某種型號的長方形材料如圖Ⅱ所示,其周長為4m,這種材料沿其對角線折疊后就出現圖Ⅰ的情況.如圖,ABCD(AB>AD)為長方形的材料,沿AC折疊后AB'交DC于點P,設△ADP的面積為
某工藝品廠要設計一個如圖Ⅰ所示的工藝品,現有某種型號的長方形材料如圖Ⅱ所示,其周長為4m,這種材料沿其對角線折疊后就出現圖Ⅰ的情況.如圖,ABCD(AB>AD)為長方形的材料,沿AC折疊后AB'交DC于點P,設△ADP的面積為分析 (Ⅰ)設AB=xm,利用△ADP≌△CB'P,故PA=PC=x-y,結合PA2=AD2+DP2,即可用x表示圖中DP的長度,并寫出x的取值范圍;
(Ⅱ)利用基本不等式求面積S2最大時,設計材料的長和寬;
(Ⅲ)求面積(S1+2S2),利用導數確定函數的單調性,即可得出最大時,設計材料的長和寬.
解答 解:(Ⅰ)由題意,AB=x,BC=2-x,
因為x>2-x,故1<x<2.…(2分)
設DP=y,則PC=x-y,
因為△ADP≌△CB'P,故PA=PC=x-y,
由PA2=AD2+DP2,得(x-y)2=(2-x)2+y2,$y=2({1-\frac{1}{x}}),1<x<2$.…(4分)
(Ⅱ)記△ADP的面積為S2,則${S_2}=({1-\frac{1}{x}})({2-x})$…(5分)
=$3-({x+\frac{2}{x}})≤3-2\sqrt{2}$,
當且僅當$x=\sqrt{2}∈({1,2})$時,S2取得最大值.…(7分)
故當材料長為$\sqrt{2}m$,寬為$({2-\sqrt{2}})m$時,S2最大.…(8分)
(Ⅲ)${S_1}+2{S_2}=\frac{1}{2}x({2-x})+({1-\frac{1}{x}})({2-x})=3-\frac{1}{2}({{x^2}+\frac{4}{x}})$,1<x<2.
于是$({{S_1}+2{S_2}})'=-\frac{1}{2}({2x-\frac{4}{x^2}})=\frac{{-{x^3}+2}}{x^2}=0$,∴$x=\root{3}{2}$.…(11分)
關于x的函數(S1+2S2)在$({1,\root{3}{2}})$上遞增,在$({\root{3}{2},2})$上遞減,
所以當$x=\root{3}{2}$時,S1+2S2取得最大值.…(12分)
故當材料長為$\root{3}{2}$m,寬為$({2-\root{3}{2}})$m時,S1+2S2最大.…(13分)
點評 本題考查利用數學知識解決實際問題,考查基本不等式,導數知識的運用,確定函數的表達式是關鍵.


科目:高中數學 來源: 題型:填空題
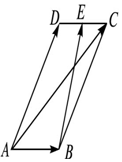 在平行四邊形ABCD中,AD=1,∠BAD=60°,E為CD的中點.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,則AB的長為$\frac{1}{4}$.
在平行四邊形ABCD中,AD=1,∠BAD=60°,E為CD的中點.若$\overrightarrow{AC}$•$\overrightarrow{BE}$=$\frac{33}{32}$,則AB的長為$\frac{1}{4}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 16 | B. | 8 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{m}{n}$ | B. | $\frac{n}{1-m}$ | C. | $\frac{1-n}{m}$ | D. | $\frac{1+n}{1+m}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com