一区视频在线,久久99深爱久久99精品,国产高清精品一区

精英家教網 > 高中數學 > 題目詳情

【題目】已知，函數.

（1）若函數在上為減函數，求實數的取值范圍；

（2）令，已知函數，若對任意，總存在，使得成立，求實數的取值范圍.

【答案】(1) .(2) .

【解析】試題分析：（1）由條件知函數單調遞減則則需在上恒成立,即在上恒成立，轉化為求函數最值問題。（2）若對任意，總存在.使得成立，則，函數在的值域是在的值域的子集.分別求兩個函數的值域，轉化為集合間的包含關系即可。

（1）因為，

要使在為減函數，則需在上恒成立.

即在上恒成立，

因為在為增函數，所以在的最小值為，

所以.

（2）因為，所以.

，

當時，，在上為遞增，

當時，，在上為遞減，

所以的最大值為，

所以的值域為.

若對任意，總存在.使得成立，則，

函數在的值域是在的值域的子集.

對于函數，

①當時，的最大值為，所以在上的值域為，

由得；

②當時，的最大值為，所以在上的值域為，

由得或 (舍）.

綜上所述，的取值范圍是.

練習冊系列答案

創新成功學習快樂寒假云南科技出版社系列答案

快樂假期寒假作業內蒙古人民出版社系列答案

快樂假期寒假作業新疆人民出版社系列答案

導學導思導練寒假評測新疆科學技術出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】如圖，為圓柱的母線，是底面圓的直徑，是的中點.

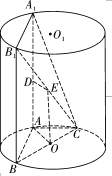
（Ⅰ）問：上是否存在點使得平面？請說明理由；

（Ⅱ）在（Ⅰ）的條件下，若平面，假設這個圓柱是一個大容器，有條體積可以忽略不計的小魚能在容器的任意地方游弋，如果小魚游到四棱錐外會有被捕的危險，求小魚被捕的概率.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】橢圓經過為坐標原點，線段的中點在圓上.

（1）求的方程；

（2）直線不過曲線的右焦點，與交于兩點，且與圓相切，切點在第一象限，的周長是否為定值？并說明理由.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知等式x4＋a1x3＋a2x2＋a3x＋a4＝(x＋1)4＋b1(x＋1)3＋b2(x＋1)2＋b3(x＋1)＋b4，定義映射f：(a1，a2，a3，a4)→(b1，b2，b3，b4)，則f(4,3,2,1)＝(　　)

A. (1,2,3,4) B. (0,3,4,0)

C. (0，－3,4，－1) D. (－1,0,2，－2)

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某公司為了解用戶對其產品的滿意度，從A、B兩地區分別隨機調查了20個用戶，得到用戶對產品的滿意度評分如下：

A地區：	62	73	81	92	95	85	74	64	53	76
	78	86	95	66	97	78	88	82	76	89
B地區：	73	83	62	51	91	46	53	73	64	82
	93	48	95	81	74	56	54	76	65	79

（Ⅰ）根據兩組數據完成兩地區用戶滿意度評分的莖葉圖，并通過莖葉圖比較兩地區滿意度的平均值及分散程度（不要求算出具體值，給出結論即可）：

（Ⅱ）根據用戶滿意度評分，將用戶的滿意度從低到高分為三個等級：

滿意度評分	低于70分	70分到89分	不低于90分
滿意度等級	不滿意	滿意	非常滿意

記事件C：“A地區用戶的滿意度等級高于B地區用戶的滿意度等級”，假設兩地區用戶的評價結果相互獨立，根據所給數據，以事件發生的頻率作為相應事件發生的概率，求C的概率。

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】2017年，世界乒乓球錦標賽在德國的杜賽爾多夫舉行．整個比賽精彩紛呈，參賽選手展現出很高的競技水平，為觀眾奉獻了多場精彩對決．圖1（扇形圖）和表1是其中一場關鍵比賽的部分數據統計．兩位選手在此次比賽中擊球所使用的各項技術的比例統計如圖1．在乒乓球比賽中，接發球技術是指回接對方發球時使用的各種方法．選手乙在比賽中的接發球技術統計如表1，其中的前4項技術統稱反手技術，后3項技術統稱為正手技術．