
分析 (I)根據<$\sqrt{2}$>的定義和$\sqrt{2}$的范圍依次計算a1,a2,a3,即可得出結論;
(II)根據定義可知$\frac{1}{2}<a<1$,依次計算a1,a2,列方程即可解出a的值.
解答 解:(I)∵1$<\sqrt{2}$<3,
∴a1=<$\sqrt{2}$>=$\sqrt{2}$-1,
∴$\frac{1}{{a}_{1}}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}+1$,
∵2$<\sqrt{2}+1<3$,
∴a2=<$\sqrt{2}+1$>=$\sqrt{2}+1-2$=$\sqrt{2}$-1,
同理可得:a3=a4=…=an=$\sqrt{2}-1$,
∴an=$\sqrt{2}$-1,
(II)∵a1=<a>=a,∴a<1,
又$a>\frac{1}{2}$,∴1$<\frac{1}{a}<2$,
∴a2=<$\frac{1}{{a}_{1}}$>=<$\frac{1}{a}$>=$\frac{1}{a}-1$,
∵a2=a,
∴$\frac{1}{a}-1=a$,解得a=$\frac{\sqrt{5}-1}{2}$.
故答案為(I)${a_n}=\sqrt{2}-1$,(II)$\frac{{\sqrt{5}-1}}{2}$.
點評 本題考查了對新定義的理解,數列的通項公式的計算,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 函數g(x)是奇函數 | B. | 函數g(x)在區間[π,2π]上是增函數 | ||
| C. | 函數g(x)的最小正周期是4π | D. | 函數g(x)的圖象關于直線x=π對稱 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
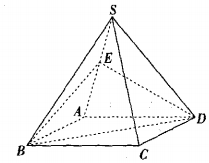 如圖,四棱錐S-ABCD中,底面ABCD為平行四邊形,E是SA的上一點,當點E滿足條件SE=EA,時,SC∥平面EBD,寫出條件并加以證明.
如圖,四棱錐S-ABCD中,底面ABCD為平行四邊形,E是SA的上一點,當點E滿足條件SE=EA,時,SC∥平面EBD,寫出條件并加以證明.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ¬p為:?x∈(-2,2),|x-1|+|x+2|<6 | B. | ¬p為:?x∈(-2,2),|x-1|+|x+2|≥6 | ||
| C. | ¬p為:?x∈(-∞,-2]∪[2,+∞),|x-1|+|x+2|<6 | D. | ¬p為真命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com