
分析 根據函數對稱變換法則,可判斷①;根據函數的對稱性,可判斷②④;根據函數的周期性,可判斷③.
解答 解:設函數y=f(-1-x)與y=f(x-1)的圖象關于直線x=a對稱,
則f[-1-(2a-x)]=f(x-1),即2a-1=-1,解得:a=0,
即函數y=f(-1-x)與y=f(x-1)的圖象關于直線x=0對稱,故①正確;
若f(1-x)=f(x-1),則函數y=f(x)的圖象關于直線x=$\frac{1-1}{2}$=0對稱,故②錯誤;
③若f(1+x)=f(x-1),f(x+2)=f[1+(1+x)]=f[(1+x)-1}=f(x),
則函數y=f(x)是周期為2的周期函數,故③正確;
④若f(1-x)=-f(x-1),則函數y=f(x)的圖象關于點(0,0)對稱,故④正確.
故答案為:①③④
點評 若f(a-x)=f(b+x)則函數圖象關于直線x=$\frac{a+b}{2}$對稱;若f(a-x)+f(b+x)=2c,則函數圖象關于($\frac{a+b}{2}$,c)對稱;若f(a+x)=f(b+x),則函數的周期為|a-b|.


科目:高中數學 來源: 題型:解答題
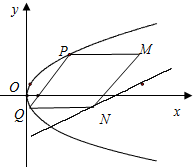 拋物線有光學性質,即由其焦點射出的光線經拋物線反射后,沿平行于拋物線對稱軸的方向射出,反之亦然.如圖所示,今有拋物線y2=2px(p>0),一光源在點M($\frac{41}{4}$,4)處,由其發出的光線沿平行于拋物線的軸的方向射向拋物線上的點P,反射后,又射向拋物線上的點Q,再反射后又沿平行于拋物線的軸的方向射出,途中遇到直線l:2x-4y-17=0上的點N,再反射后又射回點M,設P,Q兩點的坐標分別是(x1,y1),(x2,y2),
拋物線有光學性質,即由其焦點射出的光線經拋物線反射后,沿平行于拋物線對稱軸的方向射出,反之亦然.如圖所示,今有拋物線y2=2px(p>0),一光源在點M($\frac{41}{4}$,4)處,由其發出的光線沿平行于拋物線的軸的方向射向拋物線上的點P,反射后,又射向拋物線上的點Q,再反射后又沿平行于拋物線的軸的方向射出,途中遇到直線l:2x-4y-17=0上的點N,再反射后又射回點M,設P,Q兩點的坐標分別是(x1,y1),(x2,y2),查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $f(x)={log_2}(\sqrt{{x^2}+1}-x)$ | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=x2-x3 | D. | f(x)=sinx |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com