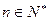(本小題滿分12分)已知各項均為正數的數列{
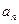
}的前n項和滿足
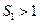
,且
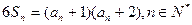
(1)求{
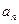
}的通項公式;(5分)
(2)設數列{
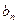
}滿足
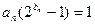
,并記
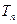
為{
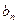
}的前n項和,
求證:
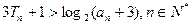
. (7分)
(I)解:由
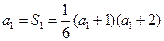
,解得
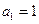
或
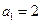
,由假設
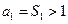
,因此
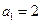
,
又由
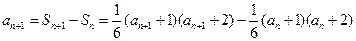
,
得
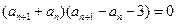
,
即
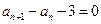
或
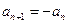
,因
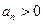
,故
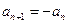
不成立,舍去.
因此
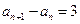
,從而
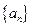
是公差為
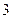
,首項為
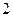
的等差數列,
故
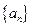
的通項為
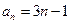
.
(II)證法一:由
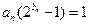
可解得
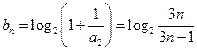
;
從而
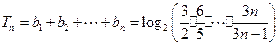
.
因此
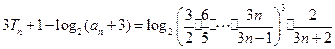
.
令
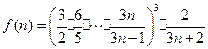
,則
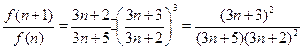
.
因
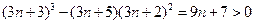
,故
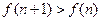
.
特別地
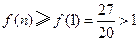
,從而
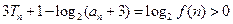
.
即
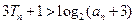
.
證法二:同證法一求得
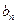
及
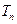
,
由二項式定理知,當
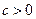
時,不等式
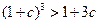
成立.
由此不等式有
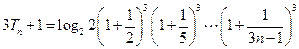
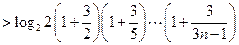
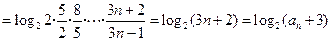
.
證法三:同證法一求得
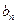
及
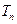
.
令
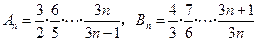
,
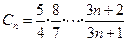
.
因
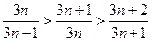
.因此
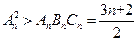
.
從而
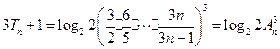
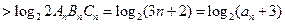
.
證法四:同證法一求得
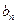
及
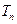
.
下面用數學歸納法證明:
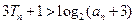
.
當
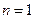
時,
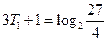
,
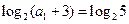
,
因此
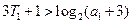
,結論成立.
假設結論當
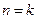
時成立,即
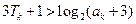
.
則當
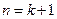
時,
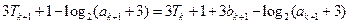
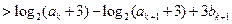
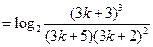
因
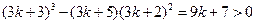
.故
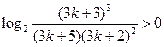
.
從而
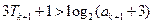
.這就是說,當
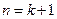
時結論也成立.
綜上
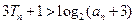
對任何
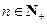
成立.
(I)解:由
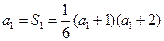
,解得
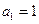
或
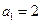
,由假設
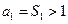
,因此
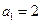
,
又由
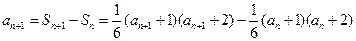
,
得
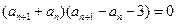
,
即
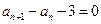
或
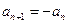
,因
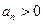
,故
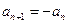
不成立,舍去.
因此
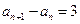
,從而
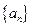
是公差為
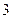
,首項為
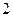
的等差數列,
故
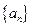
的通項為
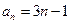
.
(II)證法一:由
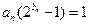
可解得
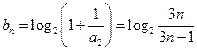
;
從而
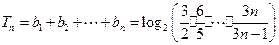
.
因此
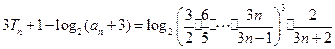
.
令
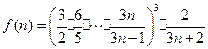
,則
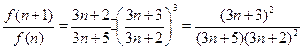
.
因
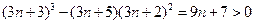
,故
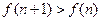
.
特別地
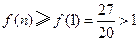
,從而
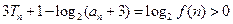
.
即
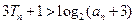
.
證法二:同證法一求得
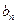
及
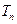
,
由二項式定理知,當
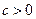
時,不等式
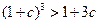
成立.
由此不等式有
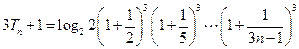
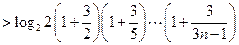
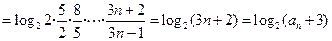
.
證法三:同證法一求得
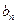
及
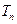
.
令
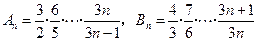
,
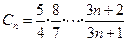
.
因
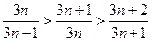
.因此
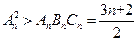
.
從而
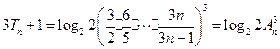
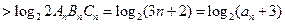
.
證法四:同證法一求得
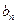
及
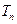
.
下面用數學歸納法證明:
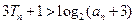
.
當
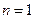
時,
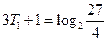
,
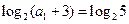
,
因此
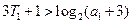
,結論成立.
假設結論當
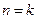
時成立,即
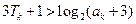
.
則當
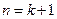
時,
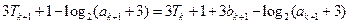
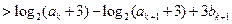
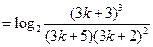
因
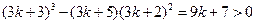
.故
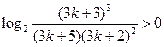
.
從而
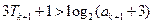
.這就是說,當
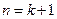
時結論也成立.
綜上
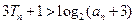
對任何
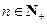
成立.
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12分)
數列
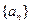
為等差數列,
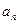
為正整數,其前
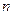
項和為
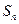
,數列
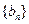
為等比數列,且
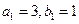
,數列
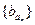
是公比為64的等比數列,
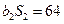
。
(1)求
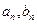
;
(2)求證
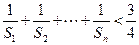
。
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列
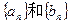
中,
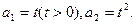
當
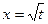
時,函數
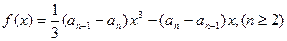
取得極值。
(1)求數列
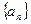
的通項公式。(6分)
(2)若點
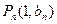
。過函數
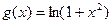
圖象上的點
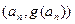
的切線始終與
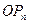
平行(O是坐標原點)。求證:當
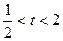
時,不等式
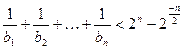
對任意
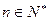
都成立。(8分)
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
若數列
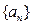
中,
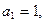
點
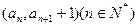
在函數
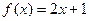
的圖像上,
(1)求數列
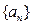
的通項公式;
(2)求數列
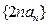
的前n項和
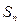
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(13分)正項數列
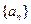
的前
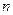
項和為
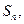
且
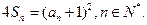
(1)試求數列
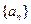
的通項公式;(2)設
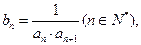
求數列
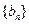
的前
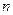
項和
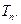
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知數列
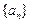
滿足:
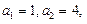
且對任意的
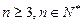
有
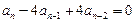
.
(Ⅰ)求數列
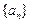
的通項公式
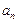
;
(Ⅱ)是否存在等差數列
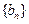
,使得對任意的
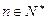
有
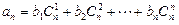
成立?證明你的結論
查看答案和解析>>
主站蜘蛛池模板:
国产精品免费久久
|
青青青国产精品一区二区
|
国产精品久久久久久久娇妻
|
久久亚洲国产精品
|
中文字幕在线精品
|
亚洲精品久久久久久久久
|
热久久这里只有精品
|
四虎影视网址
|
欲色av|
国产精选视频
|
国产精品毛片
|
免费黄在线观看
|
一区二区三区视频在线观看
|
中文字国产精久久无
|
国产精品视频一区二区三区不卡
|
在线免费自拍
|
国产美女高潮一区二区三区
|
国产一级毛片国语一级
|
久久久久久国产精品
|
全黄大全大色全免费大片
|
午夜影院a|
成人区一区二区三区
|
日韩久久一区二区
|
成人一区二区三区
|
一级黄色短片
|
日本视频一区二区
|
在线观看日韩av
|
91麻豆精品国产91久久久更新资源速度超快
|
精品免费视频一区二区
|
黄a在线
|
精品国产欧美一区二区
|
亚洲黄色免费在线看
|
欧美性一区二区三区
|
欧美日韩国产一区二区三区不卡
|
涩涩操|
国产亚洲网站
|
久久黄色|
91精品国产精品
|
日韩成人在线观看
|
99精品久久久久
|
欧美日韩电影一区二区
|

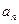 }的前n項和滿足
}的前n項和滿足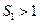 ,且
,且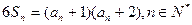
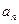 }的通項公式;(5分)
}的通項公式;(5分)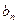 }滿足
}滿足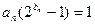 ,并記
,并記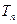 為{
為{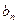 }的前n項和,
}的前n項和,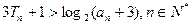 . (7分)
. (7分)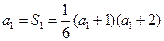 ,解得
,解得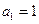 或
或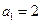 ,由假設
,由假設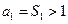 ,因此
,因此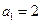 ,
,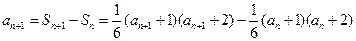 ,
,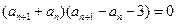 ,
,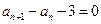 或
或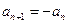 ,因
,因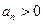 ,故
,故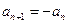 不成立,舍去.
不成立,舍去.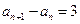 ,從而
,從而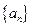 是公差為
是公差為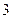 ,首項為
,首項為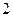 的等差數列,
的等差數列,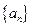 的通項為
的通項為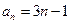 .
.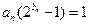 可解得
可解得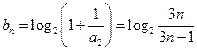 ;
;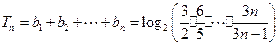 .
.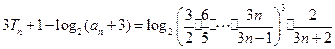 .
.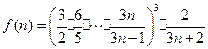 ,則
,則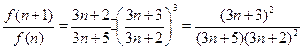 .
.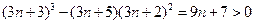 ,故
,故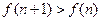 .
.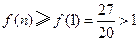 ,從而
,從而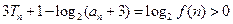 .
.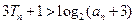 .
.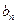 及
及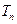 ,
,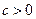 時,不等式
時,不等式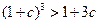 成立.
成立.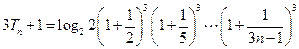
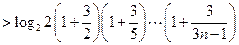
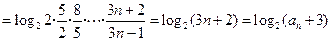 .
.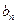 及
及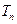 .
.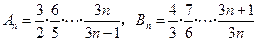 ,
,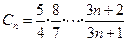 .
.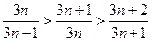 .因此
.因此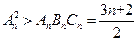 .
.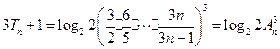
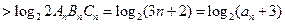 .
.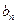 及
及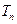 .
.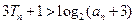 .
.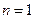 時,
時,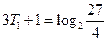 ,
,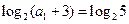 ,
,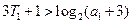 ,結論成立.
,結論成立.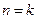 時成立,即
時成立,即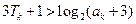 .
.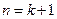 時,
時,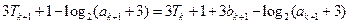
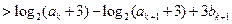
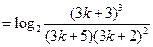
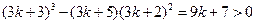 .故
.故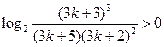 .
.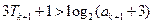 .這就是說,當
.這就是說,當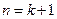 時結論也成立.
時結論也成立.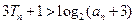 對任何
對任何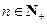 成立.
成立.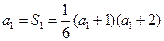 ,解得
,解得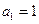 或
或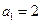 ,由假設
,由假設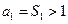 ,因此
,因此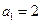 ,
,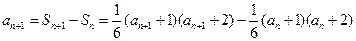 ,
,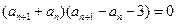 ,
,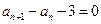 或
或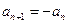 ,因
,因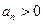 ,故
,故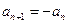 不成立,舍去.
不成立,舍去.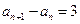 ,從而
,從而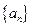 是公差為
是公差為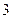 ,首項為
,首項為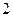 的等差數列,
的等差數列,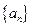 的通項為
的通項為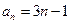 .
.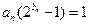 可解得
可解得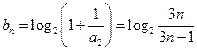 ;
;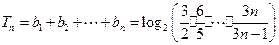 .
.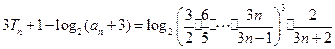 .
.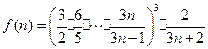 ,則
,則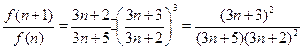 .
.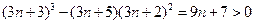 ,故
,故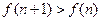 .
.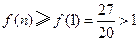 ,從而
,從而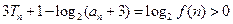 .
.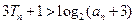 .
.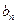 及
及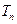 ,
,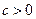 時,不等式
時,不等式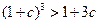 成立.
成立.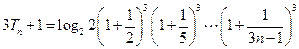
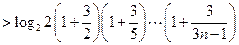
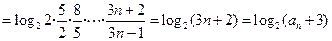 .
.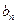 及
及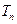 .
.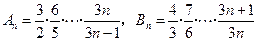 ,
,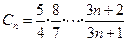 .
.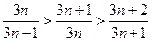 .因此
.因此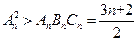 .
.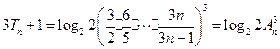
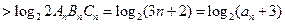 .
.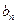 及
及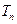 .
.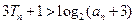 .
.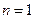 時,
時,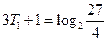 ,
,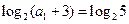 ,
,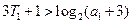 ,結論成立.
,結論成立.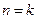 時成立,即
時成立,即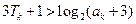 .
.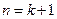 時,
時,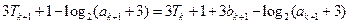
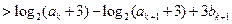
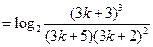
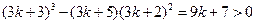 .故
.故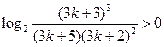 .
.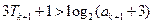 .這就是說,當
.這就是說,當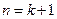 時結論也成立.
時結論也成立.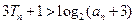 對任何
對任何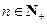 成立.
成立.

 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案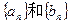 中,
中,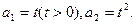 當
當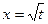 時,函數
時,函數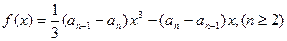 取得極值。
取得極值。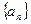 的通項公式。(6分)
的通項公式。(6分)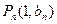 。過函數
。過函數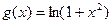 圖象上的點
圖象上的點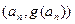 的切線始終與
的切線始終與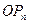 平行(O是坐標原點)。求證:當
平行(O是坐標原點)。求證:當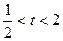 時,不等式
時,不等式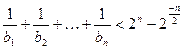 對任意
對任意