
【題目】已知函數![]() ,其中
,其中![]() ,
,![]() 為自然對數的底數.
為自然對數的底數.
(1)討論![]() 的單調性;
的單調性;
(2)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)見解析;(2)![]()
【解析】分析:(1)求出導函數![]() ,對
,對![]() 按
按![]() 和
和![]() 分類后可確定
分類后可確定![]() 的正負,即得
的正負,即得![]() 的單調區間;
的單調區間;
(2)由(1)![]() 的極值點是
的極值點是![]() ,因此在
,因此在![]() 時,函數在
時,函數在![]() 上單調遞增,當
上單調遞增,當![]() 時,可證
時,可證![]() (用導數的知識證明),然后比較
(用導數的知識證明),然后比較![]() 和
和![]() 的大小,最終求得最大值.
的大小,最終求得最大值.
詳解:(1)![]() ,
,![]() .
.
當![]() 時,
時,![]() ,則
,則![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,令
時,令![]() ,得
,得![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
綜上,當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
(2)![]() ,令
,令![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,由(1)的結論可知函數
,由(1)的結論可知函數![]() 在
在![]() 上單調遞增,
上單調遞增,![]() .
.
當![]() 時,
時,![]() ,下證
,下證![]() .事實上,令
.事實上,令![]() ,
,
則![]() .當
.當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 為增函數,且
為增函數,且
![]() ,即當
,即當![]() 時,
時,![]() 恒成立.
恒成立.
由(1)的結論,知![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
所以![]() 在
在![]() 上的最大值等于
上的最大值等于![]() .
.
設![]() ,則
,則![]()
令![]() ,易得
,易得![]() ,因為
,因為![]() ,且
,且![]() 在
在![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]() ,即
,即![]() 恒成立,所以
恒成立,所以![]() 在在
在在![]() 上單調遞增,所以
上單調遞增,所以![]() 在
在![]() 上成立,即
上成立,即![]() .因此,當
.因此,當![]() 時,
時,![]() 在
在![]() 上的最大值為
上的最大值為![]() .
.
綜上所述,當![]() 時,
時,![]() .
.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源: 題型:
【題目】![]() 市積極倡導學生參與綠色環保活動,其中代號為“環保衛士-
市積極倡導學生參與綠色環保活動,其中代號為“環保衛士-![]() ”的綠色環保活動小組對
”的綠色環保活動小組對![]() 年
年![]() 月-
月-![]() 年
年![]() 月(一月)內空氣質量指數
月(一月)內空氣質量指數![]() 進行監測,如表是在這一年隨機抽取的
進行監測,如表是在這一年隨機抽取的![]() 天的統計結果:
天的統計結果:
指數 |
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕微污染 | 輕微污染 | 中度污染 | 中重度污染 | 重度污染 |
天數 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(Ⅰ)若![]() 市某企業每天由空氣污染造成的經濟損失
市某企業每天由空氣污染造成的經濟損失![]() (單位:元)與空氣質量指數
(單位:元)與空氣質量指數![]() (記為
(記為![]() )的關系為:
)的關系為: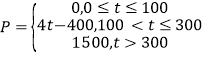 ,,在這一年內隨機抽取一天,估計該天經濟損失
,,在這一年內隨機抽取一天,估計該天經濟損失![]() 元的概率;
元的概率;
(Ⅱ)若本次抽取的樣本數據有![]() 天是在供暖季節,其中有
天是在供暖季節,其中有![]() 天為重度污染,完成
天為重度污染,完成![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為
的把握認為![]() 市本年度空氣重度污染與供暖有關?
市本年度空氣重度污染與供暖有關?

下面臨界值表供參考.
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
參考公式:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,動點M到兩定點A(﹣1,0)、B(2,0)構成△MAB,且∠MBA=2∠MAB,設動點M的軌跡為C. 
(1)求軌跡C的方程;
(2)設直線y=﹣2x+m與y軸交于點P,與軌跡C相交于點Q、R,且|PQ|<|PR|,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 總決賽采用7場4勝制,2018年總決賽兩支球隊分別為勇士和騎士,假設每場比賽勇士獲勝的概率為0.7,騎士獲勝的概率為0.3,且每場比賽的結果相互獨立,則恰好5場比賽決出總冠軍的概率為__________.
總決賽采用7場4勝制,2018年總決賽兩支球隊分別為勇士和騎士,假設每場比賽勇士獲勝的概率為0.7,騎士獲勝的概率為0.3,且每場比賽的結果相互獨立,則恰好5場比賽決出總冠軍的概率為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合![]() ,其中
,其中![]() .
.
(1)寫出集合![]() 中的所有元素;
中的所有元素;
(2)設![]() ,證明“
,證明“![]() ”的充要條件是“
”的充要條件是“![]() ”
”
(3)設集合![]() ,設
,設![]() ,使得
,使得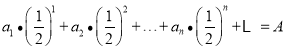 ,且
,且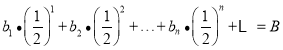 ,試判斷“
,試判斷“![]() ”是“
”是“![]() ”的什么條件并說明理由.
”的什么條件并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是公比不為1的等比數列,其前n項和為Sn , 且a5 , a3 , a4成等差數列.
(1)求數列{an}的公比;
(2)證明:對任意k∈N+ , Sk+2 , Sk , Sk+1成等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖 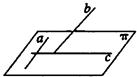
(1)證明命題“a是平面π內的一條直線,b是π外的一條直線(b不垂直于π),c是直線b在π上的投影,若a⊥b,則a⊥c”為真.
(2)寫出上述命題的逆命題,并判斷其真假(不需要證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,P是正四面體V-ABC的面VBC上一點,點P到平面ABC距離與到點V的距離相等,則動點P的軌跡是( )
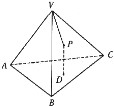
A. 直線 B. 拋物線
C. 離心率為![]() 的橢圓 D. 離心率為3的雙曲線
的橢圓 D. 離心率為3的雙曲線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)若函數f(x)=ax2-x-1有且僅有一個零點, 求實數a的值.
(2)若函數f(x)=|4x-x2|+a有4個零點,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com