
 如圖,在長方體ABCD-A1B1C1D1中,AB=AA1=1,E為BC中點.
如圖,在長方體ABCD-A1B1C1D1中,AB=AA1=1,E為BC中點.分析 (1)以D為原點,建立空間直角坐標系D-xyz,利用向量法能證明C1D⊥D1E.
(2)求出平面AD1E的法向量和平面B1AE的法向量,由二面角B1AED1的大小為90°,能求出AD的長.
解答 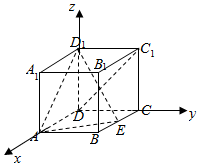 證明:(1)以D為原點,建立如圖所示的空間直角坐標系D-xyz,
證明:(1)以D為原點,建立如圖所示的空間直角坐標系D-xyz,
設AD=a,則D(0,0,0),A(a,0,0),B(a,1,0),C(0,1,0),
B1(a,1,1),C1(0,1,1),D1(0,0,1),E($\frac{a}{2}$,1,0),
∴$\overrightarrow{{C}_{1}D}$=(0,-1,-1),$\overrightarrow{{D}_{1}E}$=($\frac{a}{2}$,1,-1),
則$\overrightarrow{{C}_{1}D}$•$\overrightarrow{{D}_{1}E}$=0,
∴C1D⊥D1E.….(5分)
解:(2)設平面AD1E的法向量為$\overrightarrow{n}$=(x,y,z),
$\overrightarrow{AE}$=(-$\frac{a}{2}$,1,0),$\overrightarrow{A{D}_{1}}$=(-a,0,1),
則$\left\{\begin{array}{l}{\overrightarrow{AE}•\overrightarrow{n}=-\frac{a}{2}x+y=0}\\{\overrightarrow{A{D}_{1}}•\overrightarrow{n}=-ax+z=0}\end{array}\right.$,取x=2,得平面AD1E的一個法向量為$\overrightarrow{n}$=(2,a,2a),…..(8分)
設平面B1AE的法向量為$\overrightarrow{m}$=(x′,y′,z′),
$\overrightarrow{AE}$=(-$\frac{a}{2}$,1,0),$\overrightarrow{A{B}_{1}}$=(0,1,1),
則$\left\{\begin{array}{l}{\overrightarrow{AE}•\overrightarrow{m}=-\frac{a}{2}{x}^{'}+{y}^{'}=0}\\{\overrightarrow{A{B}_{1}}•\overrightarrow{m}={y}^{'}+{z}^{'}=0}\end{array}\right.$,取x′=2,得$\overrightarrow{m}$=(2,a,-a).…..(10分)
∵二面角B1AED1的大小為90°,
∴$\overrightarrow{m}$⊥$\overrightarrow{n}$,∴$\overrightarrow{m}$•$\overrightarrow{n}$=4+a2-2a2=0,
∵a>0,∴a=2,即AD=2…(12分)
點評 本題考查線線垂直的證明,考查線段長的求法,考查空間中線線、線面、面面間的位置關系等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想、函數與方程思想,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{\sqrt{2}}{5}$,$\frac{3}{5}$) | B. | ($\frac{\sqrt{2}}{5}$,$\frac{\sqrt{5}}{5}$) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{3}{5}$) | D. | (0,$\frac{\sqrt{5}}{5}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{5π}{6}$ | D. | x=$\frac{5π}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 為了調查喜歡旅游是否與性別有關,調查人員就“是否喜歡旅游”這個問題,在火車站分別隨機調研了50名女性和50名男性,根據調研結果得到如圖所示的等高條形圖
為了調查喜歡旅游是否與性別有關,調查人員就“是否喜歡旅游”這個問題,在火車站分別隨機調研了50名女性和50名男性,根據調研結果得到如圖所示的等高條形圖| 喜歡旅游 | 不喜歡旅游 | 合計 | |
| 女性 | |||
| 男性 | |||
| 合計 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com