Question

17．在平面直角坐標系xOy中，已知點P（0，1）在圓C：x²+y²+2mx-2y+m²-4m+1=0內，若存在過點P的直線交圓C于A、B兩點，且△PBC的面積是△PAC的面積的2倍，則實數m的取值范圍為（$\frac{4}{9}$，4）．

Answer 1

分析 由點P（0，1）在圓C內，得0＜m＜4，推導出圓心C（-m，1）PB=2PA，設直線l的方程為：y=kx+1．求出圓心C到直線l的距離，從而得到9m²-4m=10d²=10×$\frac{{k}^{2}{m}^{2}}{1+{k}^{2}}$，由此能求出實數m的取值范圍．

解答 解：點P（0，1）在圓C：x²+y²+2mx-2y+m²-4m+1=0內，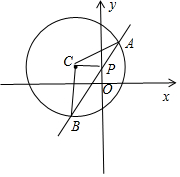
∴1-2+m²-4m+1＜0，
解得0＜m＜4；
又圓C化為標準方程是（x+m）²+（y-1）²=4m，圓心C（-m，1）；
∵△PBC的面積是△PAC的面積的2倍，
∴PB=2PA，
設直線l的方程為：y=kx+1．
圓心C到直線l的距離d=$\frac{|-km-1+1|}{\sqrt{1+{k}^{2}}}$=$\frac{|km|}{\sqrt{1+{k}^{2}}}$．
∴$\sqrt{4m-p9vv5xb5^{2}}$=3$\sqrt{{m}^{2}-p9vv5xb5^{2}}$，可得：9m²-4m=10d²=10×$\frac{{k}^{2}{m}^{2}}{1+{k}^{2}}$，
∴9-$\frac{4}{m}$=$\frac{10{k}^{2}}{1+{k}^{2}}$∈（0，10），
解得：$\frac{4}{9}≤m＜4$．
當m=$\frac{4}{9}$時，四點共線沒有三角形，
∴實數m的取值范圍為（$\frac{4}{9}$，4）．
故答案為：（$\frac{4}{9}$，4）．

點評 本題考查實數的取值范圍的求法，考查圓的方程、點到直線距離公式等基礎知識，考查推理論證能力、運算求解能力，考查化歸與轉化思想、函數與方程思想，是中檔題．