
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 根據新定義求得f(x)的解析式,再利用函數y=Asin(ωx+φ)的圖象變換規(guī)律,正弦函數的圖象的對稱性,求得φ的最小值.
解答 解:將函數f(x)=$|\begin{array}{l}{sinx}&{cosx}\\{1}&{\sqrt{3}}\end{array}|$=$\sqrt{3}$sinx-cosx=2sin(x-$\frac{π}{6}$)的圖象向右平移φ(φ>0)個單位后,
可得y=2sin(x-φ-$\frac{π}{6}$)的圖象.
根據所得圖象對應的函數為奇函數,可得φ+$\frac{π}{6}$=kπ,k∈Z,即φ=kπ-$\frac{π}{6}$,k∈Z,
所以φ的最小值是$\frac{5π}{6}$,
故選:D.
點評 本題主要考查新定義,函數y=Asin(ωx+φ)的圖象變換規(guī)律,正弦函數的圖象的對稱性,屬于基礎題.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業(yè)安徽少年兒童出版社系列答案
暑假作業(yè)安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
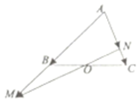 如圖所示,在△ABC中,點O是BC的中點,過點O的直線分別交直線AB,AC于不同的兩點M,N,若$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=m$\overrightarrow{AN}$,則m的值為$\frac{7}{5}$.
如圖所示,在△ABC中,點O是BC的中點,過點O的直線分別交直線AB,AC于不同的兩點M,N,若$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=m$\overrightarrow{AN}$,則m的值為$\frac{7}{5}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=x2-4x | B. | g(x)=3x+1 | C. | h(x)=3-x | D. | t(x)=tanx |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com