
分析 (Ⅰ)利用拋物線C:y2=2px(p>0)的焦點為F(1,0),求出p,即可求拋物線的方程;
(Ⅱ)設A(x1,y1),B(x2,y2),由|FA|=2|FB|,得2x2=x1-1,將直線與拋物線方程聯立可得x1+x2,x1x2 的值,解出k,從而問題得解.
解答 解:(Ⅰ)∵拋物線C:y2=2px(p>0)的焦點為F(1,0)
∴p=2,
∴拋物線的方程為y2=4x;
(Ⅱ)設直線y=k(x+1)
聯立$\left\{\begin{array}{l}{y=k(x+1)}\\{{y^2}=4x}\end{array}$得k2x2+(2k2-4)x+k2=0,
設A(x1,y1),B(x2,y2),則x1+x2=$\frac{4}{{k}^{2}}$-2①,x1x2=1②,
∵|FA|=2|FB|,∴2x2=x1-1③
①②③聯立解得k=±$\frac{2\sqrt{2}}{3}$,
∴直線方程$l:y=\frac{2}{3}\sqrt{2}(x+1)$或$l:y=-\frac{2}{3}\sqrt{2}(x+1)$
點評 本題主要考查了拋物線的標準方程和直線與拋物線的關系,考查韋達定理的運用,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | x0<a | B. | x0>b | C. | x0<c | D. | x0>c |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
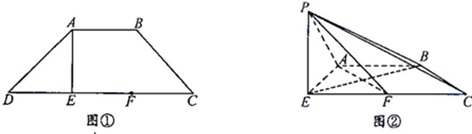
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1007 | B. | 1008 | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
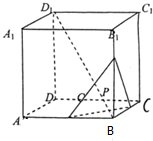 如圖,正方體ABCD-A1B1C1D1的棱長為$\sqrt{3}$,動點P在對角線BD1上,過點P作垂直于BD1的平面α,記平面α截正方體得到的截面多邊形(含三角形)的周長為y=f(x),設BP=x,x∈(0,3),關于函數y=f(x):
如圖,正方體ABCD-A1B1C1D1的棱長為$\sqrt{3}$,動點P在對角線BD1上,過點P作垂直于BD1的平面α,記平面α截正方體得到的截面多邊形(含三角形)的周長為y=f(x),設BP=x,x∈(0,3),關于函數y=f(x):查看答案和解析>>
科目:高中數學 來源: 題型:解答題
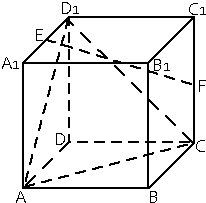 如圖在棱長為2的正方體ABCD-A1B1C1D1中,E,F分別為A1D1和CC1的中點.
如圖在棱長為2的正方體ABCD-A1B1C1D1中,E,F分別為A1D1和CC1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -1≤m≤1 | B. | m≤1 | C. | -2≤m≤2 | D. | m≥2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com