
【題目】已知函數![]() 在定義域
在定義域![]() 上的導函數為
上的導函數為![]() ,若函數
,若函數![]() 沒有零點,且
沒有零點,且![]() ,當
,當![]() 在
在![]() 上與
上與![]() 在
在![]() 上的單調性相同時,則實數
上的單調性相同時,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
由題意可知:f(x)為R上的單調函數,則f(x)﹣2019x為定值,由指數函數的性質可知f(x)為R上的增函數,則g(x)在[![]() ,
,![]() ]單調遞增,求導,則g
]單調遞增,求導,則g![]() (x)≥0恒成立,則k
(x)≥0恒成立,則k![]() sin(x
sin(x![]() )min,根據函數的正弦函數的性質即可求得k的取值范圍.
)min,根據函數的正弦函數的性質即可求得k的取值范圍.
解:若方程f![]() (x)=0無解,
(x)=0無解,
則 f′(x)>0或f′(x)<0恒成立,所以f(x)為R上的單調函數,
x∈R都有![]() ,
,
則![]() 為定值,
為定值,
設t=![]() ,則f(x)=t+
,則f(x)=t+![]() ,易知f(x)為R上的增函數,
,易知f(x)為R上的增函數,
∵g(x)=sinx﹣cosx﹣kx,
∴![]() ,
,
又g(x)與f(x)的單調性相同,
∴g(x)在R上單調遞增,則當x∈[![]() ,
,![]() ],g
],g![]() (x)≥0恒成立,
(x)≥0恒成立,
當![]() 時,
時,![]() ,
,![]() ,
,
![]() ,
,
此時k≤﹣1,
故選:A.


科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)選修4—4,坐標系與參數方程
已知曲線![]() ,直線
,直線![]() :
:![]() (
(![]() 為參數).
為參數).
(I)寫出曲線![]() 的參數方程,直線
的參數方程,直線![]() 的普通方程;
的普通方程;
(II)過曲線![]() 上任意一點
上任意一點![]() 作與
作與![]() 夾角為
夾角為![]() 的直線,交
的直線,交![]() 于點
于點![]() ,
,![]() 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某縣畜牧技術員張三和李四9年來一直對該縣山羊養殖業的規模進行跟蹤調查,張三提供了該縣某山羊養殖場年養殖數量y(單位:萬只)與相成年份x(序號)的數據表和散點圖(如圖所示),根據散點圖,發現y與x有較強的線性相關關系,李四提供了該縣山羊養殖場的個數z(單位:個)關于x的回歸方程![]() .
.

(1)根據表中的數據和所給統計量,求y關于x的線性回歸方程(參考統計量:![]() );
);
(2)試估計:①該縣第一年養殖山羊多少萬只?
②到第幾年,該縣山羊養殖的數量與第一年相比縮小了?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題:①設A,B為兩個集合,則“![]() ”是“
”是“![]() ”的充分不必要條件;②
”的充分不必要條件;②![]() ,
,![]() ;③“
;③“![]() ”是“
”是“![]() ”的充要條件;④
”的充要條件;④![]() ,代數式
,代數式![]() 的值都是質數.其中的真命題是________.(填寫序號)
的值都是質數.其中的真命題是________.(填寫序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,直線l1經過橢圓的上頂點A和右頂點B,并且和圓x2+y2=
,直線l1經過橢圓的上頂點A和右頂點B,并且和圓x2+y2=![]() 相切.
相切.
(1)求橢圓C的方程;
(2)設直線![]()
![]() 與橢圓C相交于M、N兩點,以線段OM、ON為鄰邊作平行四邊形OMPN,其中頂點P在橢圓C上,O為坐標原點,求|OP|的取值范圍.
與橢圓C相交于M、N兩點,以線段OM、ON為鄰邊作平行四邊形OMPN,其中頂點P在橢圓C上,O為坐標原點,求|OP|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在矩形ABCD中,AB=3,BC=4,E,F分別在線段BC,AD上,EF∥AB,將矩形ABEF沿EF折起,記折起后的矩形為MNEF,且平面MNEF⊥平面ECDF.
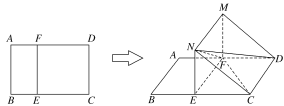
(1)在線段BC是否存在一點E,使得ND⊥FC ,若存在,求出EC的長并證明;
若不存在,請說明理由.
(2)求四面體NEFD體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 是通過某城市開發區中心O的兩條南北和東西走向的街道,鏈接M,N兩地之間的鐵路是圓心在
是通過某城市開發區中心O的兩條南北和東西走向的街道,鏈接M,N兩地之間的鐵路是圓心在![]() 上的一段圓弧,若點M在O正北方向,且
上的一段圓弧,若點M在O正北方向,且![]() ,點N到
,點N到![]() ,
,![]() 距離分別為4km和5km.
距離分別為4km和5km.
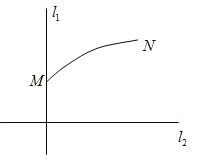
![]() 建立適當的坐標系,求鐵路線所在圓弧的方程;
建立適當的坐標系,求鐵路線所在圓弧的方程;
![]() 若該城市的某中學擬在O點正東方向選址建分校,考慮環境問題,要求校址到點O的距離大于4km,并且鐵路線上任意一點到校址的距離不能少于
若該城市的某中學擬在O點正東方向選址建分校,考慮環境問題,要求校址到點O的距離大于4km,并且鐵路線上任意一點到校址的距離不能少于![]() ,求該校址距離點O的最近距離.
,求該校址距離點O的最近距離.![]() 注:校址視為一個點
注:校址視為一個點![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com