
���}Ŀ����֪�E�AC��![]() (a>b>0)���x���ʞ�
(a>b>0)���x���ʞ�![]() ��ֱ��l1��(j��ng)�^(gu��)�E�A������c(di��n)A������c(di��n)B�����Һ͈Ax2��y2��
��ֱ��l1��(j��ng)�^(gu��)�E�A������c(di��n)A������c(di��n)B�����Һ͈Ax2��y2��![]() ���У�
����
(1)��E�AC�ķ��̣�
(2)�O(sh��)ֱ��![]()
![]() �c�E�AC�ཻ��M��N���c(di��n)���Ծ���OM��ON����߅��ƽ����߅��OMPN��������c(di��n)P�ڙE�AC�ϣ�O������(bi��o)ԭ�c(di��n)����|OP|��ȡֵ������
�c�E�AC�ཻ��M��N���c(di��n)���Ծ���OM��ON����߅��ƽ����߅��OMPN��������c(di��n)P�ڙE�AC�ϣ�O������(bi��o)ԭ�c(di��n)����|OP|��ȡֵ������
���𰸡���1��![]() ��y2��1
��y2��1
��2��[1��![]() ]
]
��������
��1��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ;��ֱ��l1�c�A
;��ֱ��l1�c�A![]() �����c
�����c![]() ,���ɽ��
,���ɽ��![]() �����ɵó���.
�����ɵó���.
��2��(li��n)��ֱ���c�E�A���O(sh��)![]() ������(j��)�f�_(d��)�����õ��c(di��n)
������(j��)�f�_(d��)�����õ��c(di��n)![]()
![]() ��
��![]() ,�������E�A�ɵõ�:
,�������E�A�ɵõ�:![]() ,����
,����![]() ������(ji��n)��
������(ji��n)��![]() ������
������![]() ,���ɵó�|OP|��ȡֵ����.
,���ɵó�|OP|��ȡֵ����.
(1)����֪�ɵ�![]() ��
��![]() ��
��![]() ������
������![]() ����
����![]() .
.
�֙E�A������c(di��n)![]() ������c(di��n)
������c(di��n)![]() ��
��
����ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����x��2y��a��0.
����x��2y��a��0.
��?y��n)�ֱ��![]() �c�A
�c�A![]() ���У����ԈA��
���У����ԈA��![]() ��ֱ��
��ֱ��![]() �ľ��x���ڈA�İ돽����
�ľ��x���ڈA�İ돽����![]() ��
��![]() �����a��2.
�����a��2.
����b��1���ʙE�AC�ķ��̞�![]() .
.
(2)��ֱ��l2�ķ��̺͙E�AC�ķ���(li��n)����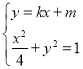
��ȥy������(ji��n)������![]() .
.
��![]() ����
����![]() .
.
�O(sh��)![]() ��
��
�t�ɸ��cϵ��(sh��)֮�g���P(gu��n)ϵ�ɵ�![]()
![]() .
.
��?y��n)���߅�?/span>OMPN��ƽ����߅�Σ�����![]() ��
��![]() .���c(di��n)P(
.���c(di��n)P(![]() ��
��![]() )��
)��
���c(di��n)P�ڙE�A�Ͽɵ� ��(
��(![]() )2��1��
)2��1��
������![]() .
.
��?y��n)?/span>![]() ������
������![]() ����
����![]()
![]() .
.![]()
�t![]() (
(![]() )2��(
)2��(![]() )2
)2
��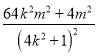 ��
��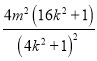 ��
��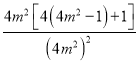
��![]() ��4��
��4��![]() .
.
��?y��n)?/span>![]() ������m2��[
������m2��[![]() ��1]������4��
��1]������4��![]() ��[1��
��[1��![]() ]����|OP|��[1��
]����|OP|��[1��![]() ]��
]��


 �p�ɊZ���ܜy(c��)�¿�ֱͨ��Уϵ�д�
�p�ɊZ���ܜy(c��)�¿�ֱͨ��Уϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У���֪
�У���֪![]() ����߅�L(zh��ng)��
����߅�L(zh��ng)��![]() �ĵ�߅�����Σ�
�ĵ�߅�����Σ�![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ƽ��
ƽ��![]() ��
��![]() �龀��
�龀��![]() ��һ��(d��ng)�c(di��n)��ӛ
��һ��(d��ng)�c(di��n)��ӛ![]() ��
��
��1����(d��ng)![]() �r(sh��)������ֱ��
�r(sh��)������ֱ��![]() �c
�c![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��2����(d��ng)![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() �r(sh��)����
�r(sh��)����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���ڶ����w![]() �У���߅��
�У���߅��![]() �������Σ�
��������![]() ��
��![]() ��
��![]() .
.

��1���C����ƽ��![]() ƽ��
ƽ��![]() .
.
��2����![]() ƽ��
ƽ��![]() �������
�������![]() ��
��![]() �������F
�������F![]() ������������
������������![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �ڶ��x��
�ڶ��x��![]() �ϵČ�(d��o)����(sh��)��
�ϵČ�(d��o)����(sh��)��![]() ��������(sh��)
��������(sh��)![]() �](m��i)�����c(di��n)����
�](m��i)�����c(di��n)����![]() ����(d��ng)
����(d��ng)![]() ��
��![]() ���c
���c![]() ��
��![]() �ϵĆ��{(di��o)����ͬ�r(sh��)���t��(sh��)��(sh��)
�ϵĆ��{(di��o)����ͬ�r(sh��)���t��(sh��)��(sh��)![]() ��ȡֵ�����ǣ� ��
��ȡֵ�����ǣ� ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
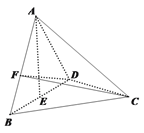
���}Ŀ���O(sh��)�E�A![]() ������c(di��n)��A������c(di��n)��B.��֪
������c(di��n)��A������c(di��n)��B.��֪![]() ��O��ԭ�c(di��n)��.
��O��ԭ�c(di��n)��.
��1����E�A���x���ʣ�
��2���O(sh��)�c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A���ڃɂ�(g��)��ͬ�c(di��n)M��N��ֱ��AM�cx�S�����c(di��n)E��ֱ��AN�cx�S�����c(di��n)F����
�c�E�A���ڃɂ�(g��)��ͬ�c(di��n)M��N��ֱ��AM�cx�S�����c(di��n)E��ֱ��AN�cx�S�����c(di��n)F����![]() .���C��ֱ��l��(j��ng)�^(gu��)���c(di��n).
.���C��ֱ��l��(j��ng)�^(gu��)���c(di��n).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ʾ��![]() ��������
��������![]() ����ƽ����һ�c(di��n)��
����ƽ����һ�c(di��n)��![]() ����
����![]() �ϵ�ͶӰ��
�ϵ�ͶӰ��![]() ��
��![]() ��
��![]() ��
��![]() ����������(g��)���}��
����������(g��)���}��
��1��![]() ��
��![]() ��
��
��2��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ��
��
��3����![]() ��
��![]() ������߅��ƽ����߅����e��32��
������߅��ƽ����߅����e��32��
��4��![]() �ă�(n��i)����돽��
�ă�(n��i)����돽��![]() .
.
�������_���}�Ă�(g��)��(sh��)�飨 ��

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
��![]() ����
����![]() ���c(di��n)������
���c(di��n)������![]() ��߅�L(zh��ng)��2�������Σ�
��߅�L(zh��ng)��2�������Σ�![]() ���������Σ�ƽ��
���������Σ�ƽ��![]() �c��
�c��![]() �����c(di��n)
�����c(di��n)![]() ��ƽ��
��ƽ��![]() �cƽ��
�cƽ��![]() ����ֱ��
����ֱ��![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() .
.

��1�����C��![]() ��
��
��2���������F![]() �ı���e.
�ı���e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���D1���ɾ���![]() ������
������![]() �M�ɵ�һ��(g��)ƽ��D�Σ�����
�M�ɵ�һ��(g��)ƽ��D�Σ�����![]() ��
�� ![]() ��������
��������![]() ����ʹ��
����ʹ��![]() �c
�c![]() �غϣ��B�Y(ji��)
�غϣ��B�Y(ji��)![]() ����D2.
����D2.
��1���C���D2�е�![]() ���c(di��n)���棬��ƽ��
���c(di��n)���棬��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����D2�е���߅��![]() ����e.
����e.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����⌍(sh��)��(sh��)![]() ��
��![]() �����x
�����x ���O(sh��)����(sh��)
���O(sh��)����(sh��)![]() ����(sh��)��
����(sh��)��![]() �ǹ��ȴ���0�ĵȱȔ�(sh��)�У���
�ǹ��ȴ���0�ĵȱȔ�(sh��)�У���![]() ��
��![]() ���t
���t![]() ____.
____.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com