
【題目】已知橢圓![]() ,記
,記![]() 為與原點距離等于
為與原點距離等于![]() 的全體直線所成的集合.問:是否存在常數
的全體直線所成的集合.問:是否存在常數![]() ,使得對任意的直線
,使得對任意的直線![]() ,均存在
,均存在![]() 、
、![]() ,
,![]() 、
、![]() 分別過
分別過![]() 與橢圓
與橢圓![]() 的交點
的交點![]() 、
、![]() ,且有
,且有![]() ?并說明理由.
?并說明理由.
【答案】![]()
【解析】
假設存在滿足題設條件的常數![]() .取
.取![]() 為特殊直線:
為特殊直線:![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
作以原點![]() 為圓心、
為圓心、![]() 為半徑的圓
為半徑的圓![]() 與
與![]() 軸的正半軸交于點
軸的正半軸交于點![]() .顯然,圓
.顯然,圓![]() 與直線
與直線![]() 切于點
切于點![]() ,且
,且![]() .
.
依題意,存在直線![]() 、
、![]() ,分別過點
,分別過點![]() 、
、![]() ,且與圓
,且與圓![]() 相切.設切點分別為
相切.設切點分別為![]() 、
、![]() .
.
則![]() 、
、![]() 分別垂直相互平行的直線
分別垂直相互平行的直線![]() 、
、![]() .故
.故![]() 為圓
為圓![]() 的直徑.
的直徑.
從而,![]() 是梯形
是梯形![]() 的中位線.
的中位線.
由![]() ,知
,知![]() ,
,![]() .
.
因此,點![]() ,且
,且![]() ,
,![]() .
.
又點![]() 在橢圓
在橢圓![]() 上,由假設知橢圓方程為
上,由假設知橢圓方程為![]() .
.
下面證明:![]() 即為所求.
即為所求.
先證明:若![]() ,且與橢圓
,且與橢圓![]() 交于點
交于點![]() 、
、![]() ,則
,則![]() .
.
設直線![]() .
.
則原點![]() 到
到![]() 的距離為
的距離為![]() .
.
故![]() .
.
將直線![]() 的方程代入橢圓方程得
的方程代入橢圓方程得![]() .
.
設![]() ,
,![]() .
.
則由韋達定理得![]() ,
,
![]() .故
.故![]()
![]()
![]()
![]() ,即
,即![]() .
.
易證,若直線![]() 的斜率不存在,則
的斜率不存在,則![]() .
.
假設![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于點
交于點![]() 與
與![]() 、
、![]() 與
與![]() .則
.則
![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
故![]() ,即
,即![]() .
.
綜上,存在唯一![]() 滿足題意.
滿足題意.


科目:高中數學 來源: 題型:
【題目】已知![]() 三個內角
三個內角![]() 所對的邊分別是
所對的邊分別是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圓半徑為2,求
的外接圓半徑為2,求![]() 周長的最大值.
周長的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)由正弦定理將邊角關系化為邊的關系![]() ,再根據余弦定理求角
,再根據余弦定理求角![]() ,(2)先根據正弦定理求邊,用角表示周長,根據兩角和正弦公式以及配角公式化為基本三角函數,最后根據正弦函數性質求最大值.
,(2)先根據正弦定理求邊,用角表示周長,根據兩角和正弦公式以及配角公式化為基本三角函數,最后根據正弦函數性質求最大值.
試題解析:(1)由正弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
因為![]() ,則
,則![]() .
.
(2)由正弦定理![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴周長![]()
![]()
![]()
![]()
![]()
![]()
∵![]() ,∴
,∴![]()
∴當![]() 即
即![]() 時
時![]()
∴當![]() 時,
時, ![]() 周長的最大值為
周長的最大值為![]() .
.
【題型】解答題
【結束】
18
【題目】經調查,3個成年人中就有一個高血壓,那么什么是高血壓?血壓多少是正常的?經國際衛生組織對大量不同年齡的人群進行血壓調查,得出隨年齡變化,收縮壓的正常值變化情況如下表:

其中:  ,
, ![]() ,
, ![]()

(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;(
;(![]() 的值精確到0.01)
的值精確到0.01)
(3)若規定,一個人的收縮壓為標準值的0.9~1.06倍,則為血壓正常人群;收縮壓為標準值的1.06~1.12倍,則為輕度高血壓人群;收縮壓為標準值的1.12~1.20倍,則為中度高血壓人群;收縮壓為標準值的1.20倍及以上,則為高度高血壓人群.一位收縮壓為180mmHg的70歲的老人,屬于哪類人群?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地統計局調查了10000名居民的月收入,并根據所得數據繪制了樣本的頻率分布直方圖如圖所示。

(1)求居民月收入在[3000,3500)內的頻率;
(2)根據頻率分布直方圖求出樣本數據的中位數;
(3)為了分析居民的月收入與年齡、職業等方面的關系,必須按月收入再從這10000中用分層抽樣的方法抽出100人做進一步分析,則應從月收入在[2500,3000)內的居民中抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某縣大潤發超市為了惠顧新老顧客,決定在2019年元旦來臨之際舉行“慶元旦,迎新年”的抽獎派送禮品活動.為設計一套趣味性抽獎送禮品的活動方案,該超市面向該縣某高中學生征集活動方案.該中學某班數學興趣小組提供的方案獲得了征用.方案如下:將一個![]() 的正方體各面均涂上紅色,再把它分割成64個相同的小正方體.經過攪拌后,從中任取兩個小正方體,記它們的著色面數之和為
的正方體各面均涂上紅色,再把它分割成64個相同的小正方體.經過攪拌后,從中任取兩個小正方體,記它們的著色面數之和為![]() ,記抽獎中獎的禮金為
,記抽獎中獎的禮金為![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ)凡是元旦當天在超市購買物品的顧客,均可參加抽獎.記抽取的兩個小正方體著色面數之和為6,設為一等獎,獲得價值50元禮品;記抽取的兩個小正方體著色面數之和為5,設為二等獎,獲得價值30元禮品;記抽取的兩個小正方體著色面數之和為4,設為三等獎,獲得價值10元禮品,其他情況不獲獎.求某顧客抽獎一次獲得的禮金的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
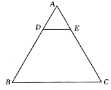
【題目】在工業生產中,對一正三角形薄鋼板(厚度不計)進行裁剪可以得到一種梯形鋼板零件,現有一邊長為3(單位:米)的正三角形鋼板(如圖),沿平行于邊![]() 的直線
的直線![]() 將
將![]() 剪去,得到所需的梯形鋼材
剪去,得到所需的梯形鋼材![]() ,記這個梯形鋼板的周長為
,記這個梯形鋼板的周長為![]() (單位:米),面積為
(單位:米),面積為![]() (單位:平方米).
(單位:平方米).
(1)求梯形![]() 的面積
的面積![]() 關于它的周長
關于它的周長![]() 的函數關系式;
的函數關系式;
(2)若在生產中,梯形![]() 的面積與周長之比(即
的面積與周長之比(即![]() )達到最大值時,零件才能符合使用要求,試確定這個梯形的周長
)達到最大值時,零件才能符合使用要求,試確定這個梯形的周長![]() 為多時,該零件才可以在生產中使用?
為多時,該零件才可以在生產中使用?
查看答案和解析>>
科目:高中數學 來源: 題型:
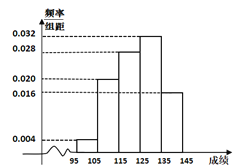
【題目】半期考試后,班長小王統計了50名同學的數學成績,繪制頻率分布直方圖如圖所示.
![]() 根據頻率分布直方圖,估計這50名同學的數學平均成績;
根據頻率分布直方圖,估計這50名同學的數學平均成績;
![]() 用分層抽樣的方法從成績低于115的同學中抽取6名,再在抽取的這6名同學中任選2名,求這兩名同學數學成績均在
用分層抽樣的方法從成績低于115的同學中抽取6名,再在抽取的這6名同學中任選2名,求這兩名同學數學成績均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其圖象的相鄰兩條對稱軸之間的距離為
,其圖象的相鄰兩條對稱軸之間的距離為![]() .
.
(1)求函數![]() 的解析式及對稱中心;
的解析式及對稱中心;
(2)將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度得到函數
個單位長度得到函數![]() 的圖象,若關于x的方程
的圖象,若關于x的方程![]() 在區間
在區間![]() 上有兩個不相等的實根,求實數m的取值范圍.
上有兩個不相等的實根,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com