
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 處取得極值,求實數
處取得極值,求實數![]() 的值;
的值;
(2)若函數![]() )在區間
)在區間![]() 上為增函數,求實數
上為增函數,求實數![]() 的取值范圍;
的取值范圍;
(3)若當![]() 時,方程
時,方程![]() 有實數根,求實數
有實數根,求實數![]() 的最大值.
的最大值.
【答案】(1) ![]() ;(2)
;(2) 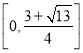 ;(3)0.
;(3)0.
【解析】試題分析:(1)函數在某一點處取得極值即該函數的導函數在該點的函數值為零;
(2)![]() 在
在![]() 上為增函數,
上為增函數, ![]() 在
在![]() 上恒成立,建立關于
上恒成立,建立關于![]() 的不等式,分類討論求解即可;
的不等式,分類討論求解即可;
(3)方程![]() 可轉化為
可轉化為![]() 在
在![]() 上有解,然后對
上有解,然后對![]() 的值域進行討論,求出
的值域進行討論,求出![]() 的取值范圍即可.
的取值范圍即可.
試題解析: (1) ![]()
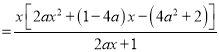 ,
,
因為函數![]() 在
在![]() 處取得極值,所以
處取得極值,所以![]() ,即
,即![]() ,解得
,解得![]() ,且經檢驗成立.
,且經檢驗成立.
(2)因為函數![]() 在區間
在區間![]() 上為增函數,
上為增函數,
所以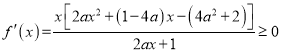 對
對![]() 恒成立.
恒成立.
討論:
當![]() 時,
時, ![]() 對
對![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上為增函數,故
上為增函數,故![]() 符合題意.
符合題意.
當![]() 時,
時, ![]() ,所以
,所以![]() ,且
,且![]() 對
對![]() 上恒成立,
上恒成立,
令![]() ,其對稱軸方程為
,其對稱軸方程為![]() ,又因為
,又因為![]() ,所以
,所以![]() ,所以要使
,所以要使
![]() 對
對![]() 上恒成立,只要
上恒成立,只要![]() 即可,即
即可,即![]() ,所以
,所以![]() .
.
又因為![]() ,所以
,所以![]() .
.
綜上,實數![]() 的取值范圍為
的取值范圍為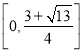 .
.
(3)當![]() 時,方程
時,方程![]() 可化為
可化為![]() .
.
所以![]() 在區間
在區間![]() 上有解.
上有解.
引入![]() ,令
,令![]() ,
,
則![]() ,
,
所以當![]() 時,
時, ![]() ,從而函數
,從而函數![]() 在
在![]() 上為增函數;
上為增函數;
當![]() 時,
時, ![]() ,從而函數
,從而函數![]() 在
在![]() 上為減函數,
上為減函數,
因此![]() .又
.又![]() ,所以當
,所以當![]() 時,
時, ![]() .
.
又![]() ,所以
,所以![]() ,因此當
,因此當![]() 時,
時, ![]() 取得最大0.
取得最大0.


 名題金卷系列答案
名題金卷系列答案科目:高中數學 來源: 題型:
【題目】某農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間的關系進行分析研究,他們分別記錄了12月1日至12月5日的每天晝夜溫差與實驗室每天每100顆種子中的發芽數,得到如下資料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差x (℃) | 10 | 11 | 13 | 12 | 8 |
發芽數y(顆) | 23 | 25 | 30 | 26 | 16 |
該農科所確定的研究方案是:先從這五組數據中選取2組,用剩下的3組數據求線性回歸方程,再對被選取的2組數據進行檢驗.
(1)若選取的是12月1日與12月5日的兩組數據,請根據12月2日至12月4日的數據,求出y關于x的線性回歸方程![]() =
=![]() x+
x+![]() ;
;
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的,試問(1)中所得的線性回歸方程是否可靠?
附: 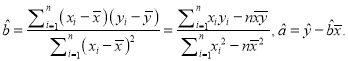
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上周某校高三年級學生參加了數學測試,年部組織任課教師對這次考試進行成績分析.現從中隨機選取了40名學生的成績作為樣本,已知這40名學生的成績全部在40分至100分之間(滿分100分,成績不低于40分),現將成績按如下方式分成6組:第一組![]() ;第二組
;第二組![]() ;……;第六組
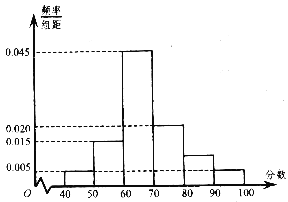
;……;第六組![]() ,并據此繪制了如圖所示的頻率分布直方圖.
,并據此繪制了如圖所示的頻率分布直方圖.
(Ⅰ)估計這次月考數學成績的平均分和眾數;
(Ⅱ)從成績大于等于80分的學生中隨機選2名,求至少有1名學生的成績在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三個臭皮匠頂上一個諸葛亮,能頂得上嗎?在一次有關“三國演義”的知識競賽中,三個臭皮匠A、B、C能答對題目的概率分別為P(A)=![]() ,P(B)=
,P(B)=![]() ,P(C)=
,P(C)=![]() ,諸葛亮D能答對題目的概率為P(D)=
,諸葛亮D能答對題目的概率為P(D)=![]() ,如果將三個臭皮匠A、B、C組成一組與諸葛亮D比賽,答對題目多者為勝方,問哪方勝?
,如果將三個臭皮匠A、B、C組成一組與諸葛亮D比賽,答對題目多者為勝方,問哪方勝?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,現提供
,現提供![]() 的大致圖象的8個選項:
的大致圖象的8個選項:
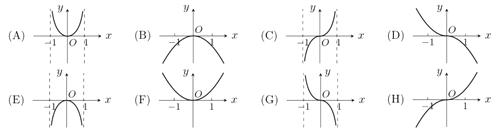
(1)請你作出選擇,你選的是( );
(2)對于函數圖像的判斷,往往只需了解函數的基本性質.為了驗證你的選擇的正確性,請你解決
下列問題:
①![]() 的定義域是___________________;
的定義域是___________________;
②就奇偶性而言, ![]() 是______________________ ;
是______________________ ;
③當![]() 時,
時, ![]() 的符號為正還是負?并證明你的結論.
的符號為正還是負?并證明你的結論.
(解決了上述三個問題,你要調整你的選項,還來得及.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了紀念“中國紅軍長征90周年”,增強學生對“長征精神”的深刻理解,在全校組織了一次有關“長征”的知識競賽,經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得20分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
, ![]() ,
, ![]() ,且各人回答正確與否相互之間沒有影響,用
,且各人回答正確與否相互之間沒有影響,用![]() 表示乙隊的總得分.
表示乙隊的總得分.
(1)求![]() 的分布列和均值;
的分布列和均值;
(2)求甲、乙兩隊總得分之和等于40分且甲隊獲勝的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com