Question

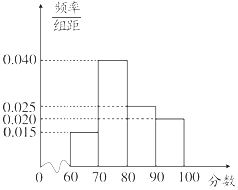
5．2016年年底，某商業集團根據相關評分標準，對所屬20家商業連鎖店進行了年度考核評估，并依據考核評估得分（最低分60分，最高分100分）將這些連鎖店分別評定為A，B，C，D四個類型，其考核評估標準如表：

評估得分	[60，70）	[70，80）	[80，90）	[90，100]
評分類型	D	C	B	A

考核評估后，對各連鎖店的評估分數進行統計分析，得其頻率分布直方圖如下：
（Ⅰ）評分類型為A的商業連鎖店有多少家；
（Ⅱ）現從評分類型為A，D的所有商業連鎖店中隨機抽取兩家做分析，求這兩家來自同一評分類型的概率．

Answer 1

分析 （Ⅰ）先求出評分類型為A的商業連鎖店所占的頻率，由此能求出評分類型為A的商業連鎖店共有多少家．
（Ⅱ）依題意評分類型為D的商業連鎖店有3家，設評分類型為A的4商業連鎖店為a₁，a₂，a₃，a₄，評分類型為D的3商業連鎖店為b₁，b₂，b₃，由此利用列舉法能求出這兩家來自同一評分類型的概率．

解答 （本小題滿分13分）
解：（Ⅰ）評分類型為A的商業連鎖店所占的頻率為0.020×10=0.2，
所以評分類型為A的商業連鎖店共有0.2×20=4家；…．（4分）
（Ⅱ）依題意評分類型為D的商業連鎖店有3家，
設評分類型為A的4商業連鎖店為a₁，a₂，a₃，a₄，
評分類型為D的3商業連鎖店為b₁，b₂，b₃，…．（6分）
從評分類型為A，D的所有商業連鎖店中隨機抽取兩家的所有可能情況有：
（a₁，a₂），（a₁，a₃），（a₁，a₄），（a₁，b₁），（a₁，b₂），（a₁，b₃），
（a₂，a₃），（a₂，a₄），（a₂，b₁），（a₂，b₂），（a₂，b₃），（a₃，a₄），
（a₃，b₁），（a₃，b₂），（a₃，b₃），（a₄，b₁），（a₄，b₂），（a₄，b₃），
（b₁，b₂），（b₁，b₃），（b₂，b₃）共21種，…．（10分）
其中滿足條件的共有9種，…．（12分）
所以這兩家來自同一評分類型的概率為$\frac{9}{21}=\frac{3}{7}$．…．（13分）

點評 本題考查頻率分布列的應用，考查概率的求法，是基礎題，解題時要認真審題，注意列舉法的合理運用．